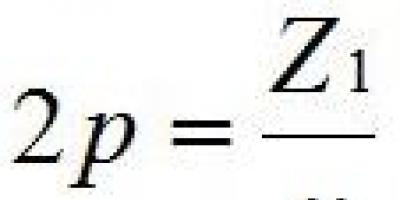need on nurkade koosinused, mille vektor teeb koordinaatide positiivsete pooltelgedega. Suunakoosinused määravad üheselt vektori suuna. Kui vektori pikkus on 1, siis on selle suunakoosinused võrdsed tema koordinaatidega. Üldiselt koordinaatidega vektori puhul ( a; b; c) suunakoosinused on võrdsed:
kus a, b, g on vektori poolt moodustatud nurgad telgedega x, y, z vastavalt.
21) Vektori lagundamine vektoritega. Koordinaatide telje orth on tähistatud , teljed - , teljed - tähega (joonis 1).
Mis tahes tasapinnal asuva vektori korral toimub järgmine lagunemine:
Kui vektor 
asub ruumis, siis on koordinaattelgede ühikvektorite laiendus järgmine:
22)Dot toode kaks nullist erinevat vektorit ja arvu, mis on võrdne nende vektorite pikkuste ja nendevahelise nurga koosinuse korrutisega, nimetatakse:
23) Kahe vektori vaheline nurk
Kui kahe vektori vaheline nurk on terav, on nende punktkorrutis positiivne; kui vektorite vaheline nurk on nüri, siis on nende vektorite skalaarkorrutis negatiivne. Kahe nullist erineva vektori skalaarkorrutis on null siis ja ainult siis, kui need vektorid on ortogonaalsed.
24) Kahe vektori paralleelsuse ja perpendikulaarsuse tingimus.
Vektorite perpendikulaarsuse tingimus
Vektorid on risti siis ja ainult siis, kui nende sisekorrutis on null.Antud on kaks vektorit a(xa;ya) ja b(xb;yb). Need vektorid on risti, kui avaldis xaxb + yayb = 0.
25) Kahe vektori vektorkorrutis.
Kahe mittekollineaarse vektori vektorkorrutis on vektor c=a×b, mis vastab järgmistele tingimustele: 1) |c|=|a| |b| sin(a^b) 2) c⊥a, c⊥b 3) Vektorid a, b, c moodustavad vektorite parempoolse kolmiku.
26) Kollineaarsed ja koplanaarsed vektorid.
Vektorid on kollineaarsed, kui esimese vektori abstsiss on seotud teise abstsissiga samamoodi nagu esimese ordinaat on teise ordinaatiga. Antud on kaks vektorit a (xa;jah) Ja b (xb;yb). Need vektorid on kollineaarsed, kui x a = xb Ja y a = yb, Kus R.
Vektorid −→ a,−→b ja −→ c helistas koplanaarne kui on olemas tasapind, millega nad on paralleelsed.
27) Kolme vektori segakorrutis. Vektorite segakorrutis- vektori a skalaarkorrutis ning vektorite b ja c vektorkorrutis. Leidke vektorite a = (1; 2; 3), b = (1; 1; 1), c = (1; 2; 1) segakorrutis.
Lahendus:
1 1 1 + 1 1 2 + 1 2 3 - 1 1 3 - 1 1 2 - 1 1 2 = 1 + 2 + 6 - 3 - 2 - 2 = 2
28) Tasapinna kahe punkti vaheline kaugus. Kahe antud punkti vaheline kaugus on võrdne nende punktide samade koordinaatide ruudu erinevuste summa ruutjuurega.
29) Segmendi jaotus selles osas. Kui punkt M(x; y) asub sirgel, mis läbib kahte antud punkti ( , ) ja ( , ) ja on antud seos, milles punkt M jagab lõigu , siis määratakse punkti M koordinaadid valemite järgi
Kui punkt M on lõigu keskpunkt, määratakse selle koordinaadid valemitega
30-31. Sirge kalle nimetatakse selle sirge kalde puutujaks. Sirge kallet tähistatakse tavaliselt tähega k. Siis definitsiooni järgi
Joone võrrand kaldega on vorm kus k- sirge nurga koefitsient, b on mingi reaalarv. Sirge ja kalde võrrand võib seada mis tahes sirge, mis ei ole teljega paralleelne Oy(y-teljega paralleelse sirge puhul ei ole kalle määratletud).
33. Tasapinna sirge üldvõrrand. Tüüpvõrrand 
Seal on sirge üldvõrrand Oxy. Sõltuvalt konstantide A, B ja C väärtustest on võimalikud järgmised erijuhud:
C \u003d 0, A ≠ 0, B ≠ 0 - joon läbib alguspunkti
A \u003d 0, B ≠ 0, C ≠ 0 (By + C \u003d 0) - joon on paralleelne Ox teljega
B \u003d 0, A ≠ 0, C ≠ 0 ( Ax + C \u003d 0) - joon on paralleelne Oy teljega
B \u003d C \u003d 0, A ≠ 0 - sirgjoon langeb kokku Oy teljega
A \u003d C \u003d 0, B ≠ 0 - sirgjoon langeb kokku Ox teljega
34.Segmentides sirgjoone võrrand tasapinnal ristkülikukujulises koordinaatsüsteemis Oxy on vorm kus a Ja b on mõned nullist erinevad reaalarvud. See nimi pole juhuslik, kuna arvude absoluutväärtused A Ja b võrdne nende lõikude pikkustega, mille sirgjoon koordinaattelgedel ära lõikab Ox Ja Oy vastavalt (segmendid loetakse lähtepunktist). Seega muudab sirgjoone võrrand segmentides lihtsaks selle sirge ehitamise joonisel. Selleks märgi punktid koordinaatidega ja ristkülikukujulises koordinaatsüsteemis tasapinnale ning ühenda need joonlauaga sirgjoonega.
35. Sirge normaalvõrrandil on vorm
kus on kaugus sirgest lähtepunktini; on nurk sirgjoone ja telje vahel.
Normaalvõrrandi saab üldvõrrandist (1), korrutades selle normaliseeriva teguriga, märk on vastupidine märgile, nii et .
Sirge ja koordinaattelgede vaheliste nurkade koosinusi nimetatakse suunakoosinusteks, on nurk sirge ja telje vahel, on sirge ja telje vahel:
Seega saab normaalvõrrandi kirjutada järgmiselt
Kaugus punktist sirgeks määratakse valemiga 
36. Punkti ja sirge vaheline kaugus arvutatakse järgmise valemiga: 
kus x 0 ja y 0 on punkti koordinaadid ning A, B ja C on sirge üldvõrrandi koefitsiendid
37. Sirge üldvõrrandi viimine normaalseks. Võrrand ja tasand selles kontekstis ei erine üksteisest millegi muu kui võrrandites olevate liikmete arvu ja ruumi mõõtme poolest. Seetõttu ütlen alguses kõik lennuki kohta ja lõpus teen reservatsiooni sirgjoone osas.
Olgu antud tasandi üldvõrrand: Ax + By + Cz + D = 0.
;. saame süsteemi: g;Mc=cosb, MB=cosaToome selle normaalkujule. Selleks korrutame mõlemad võrrandi osad normaliseeriva teguriga M. Saame: Max + Mvu + MSz + MD = 0. Sel juhul МА=cos;.g;Mc=cosb, MB=cosa saame süsteemi:
M2 B2=cos2b
M2 C2=cos2g
Kui liita kõik süsteemi võrrandid, saame M * (A2 + B2 + C2) \u003d 1 Nüüd jääb üle vaid M väljendada siit, et teada saada, millise konkreetse normaliseeriva teguriga tuleb algne üldvõrrand korrutada selle toomiseks normaalsele kujule:
M \u003d - + 1 / JUUR KV A2 + B2 + C2
MD peab alati olema väiksem kui null, seetõttu võetakse arvu M märk vastandina numbri D märgile.
Sirge võrrandiga on kõik sama, ainult termin C2 tuleks lihtsalt M valemist eemaldada.
| Ax + Kõrval + cz + D = 0, |
38.Tasapinna üldvõrrand ruumis nimetatakse vormi võrrandiks
Kus A 2 + B 2 + C 2 ≠ 0 .
Kolmemõõtmelises ruumis Descartes'i koordinaatsüsteemis kirjeldatakse mis tahes tasapinda 1. astme võrrandiga (lineaarvõrrand). Ja vastupidi, iga lineaarvõrrand määratleb tasapinna.
40.Tasapinna võrrand segmentides. Ristkülikukujulises koordinaatsüsteemis Oxyz kolmemõõtmelises ruumis vormi võrrand 
, Kus a, b Ja c kutsutakse teisi reaalarve kui null tasapinnaline võrrand segmentides. Arvude absoluutväärtused a, b Ja c võrdne nende lõikude pikkustega, mille tasapind koordinaattelgedel maha lõikab Ox, Oy Ja Oz vastavalt päritolust lugedes. Numbrimärk a, b Ja c näitab, millises suunas (positiivne või negatiivne) lõigud koordinaatide telgedele kantakse
41) Tasapinna normaalvõrrand.
Tasapinna normaalvõrrand on selle võrrand, mis on kirjutatud kujul
kus , , on tasapinna normaaljoone suunakoosinused, e
p on kaugus lähtepunktist tasapinnani. Normaali suunakoosinuste arvutamisel tuleb arvestada, et see on suunatud lähtepunktist tasapinnale (kui tasand läbib alguspunkti, siis on normaalse positiivse suuna valik ükskõikne).
42) Kaugus punktist tasapinnani.Olgu tasand antud võrrandiga 
ja andis punkti. Seejärel määratakse valemiga kaugus punktist tasapinnani
 |
Tõestus. Kaugus punktist tasapinnani on definitsiooni järgi punktist tasapinnale langenud risti pikkus
Tasapindadevaheline nurk
Laskma lennukid ja anda võrrandid ja Vastavalt. On vaja leida nende tasandite vaheline nurk.
Tasapinnad, lõikuvad, moodustavad neli kahetahulist nurka: kaks nüri ja kaks teravat või neli sirget ning mõlemad nürinurgad on üksteisega võrdsed ja mõlemad teravnurgad on samuti võrdsed. Otsime alati teravnurka. Selle väärtuse määramiseks võtame tasapindade lõikejoonel punkti ja selles punktis igas punktis
tasapinnad joonestame ristumisjoonega risti.
Olgu vektor antud. Ühikvektor samas suunas kui 
(vektor vektor 
) leitakse järgmise valemiga:
.
Laske telg 
moodustab koordinaattelgedega nurgad 
.Telje suunakoosinused 
nende nurkade koosinusi nimetatakse: Kui suund 
antud ühikvektoriga 
, siis on selle koordinaatideks suunakoosinused, st:
.
Suunakoosinused on seotud suhtega:
Kui suund 
antud suvalise vektoriga 
, seejärel leidke selle vektori ühikvektor ja võrrelge seda ühikvektori avaldisega 
, hankige:
Skalaarkorrutis
Dot toode
kaks vektorit 
Ja 
nimetatakse arvuks, mis võrdub nende pikkuste korrutisega nendevahelise nurga koosinusega: 
.
Skalaarkorrutisel on järgmised omadused:
Seega 
.
Skalaarkorrutise geomeetriline tähendus: vektori ja ühikvektori punktkorrutis 
võrdne vektori projektsiooniga 
määratud suunas 
, st. 
.
Skalaarkorrutise definitsioonist tuleneb järgmine ortide korrutamise tabel 
:
.
Kui vektorid on antud nende koordinaatidega 
Ja 
, st. 
,
, siis korrutades need vektorid skalaarselt ja kasutades ortide korrutustabelit, saame skalaarkorrutise avaldise 
vektorite koordinaatide kaudu:
.
vektorprodukt
Vektori ristkorrutis
vektori kohta 
nimetatakse vektoriks 
, mille pikkus ja suund on määratud järgmiste tingimustega:
Vektorproduktil on järgmised omadused:
Kolmest esimesest omadusest järeldub, et vektorite summa vektorkorrutamine vektorite summaga järgib tavalisi polünoomide korrutamise reegleid. Tuleb vaid jälgida, et kordajate järjekord ei muutuks.
Põhiühiku vektorid korrutatakse järgmiselt:
Kui 
Ja 
, siis, võttes arvesse vektorite vektorkorrutise omadusi, saame faktorvektorite koordinaatidest tuletada vektori korrutise koordinaatide arvutamise reegli:
Kui võtta arvesse ülaltoodud ortide korrutamise reegleid, siis:
Kahe vektori vektorkorrutise koordinaatide arvutamiseks mõeldud avaldise kirjutamise kompaktsema vormi saab konstrueerida, kui võtta kasutusele maatriksdeterminandi mõiste.
Vaatleme erijuhtumit, kui vektorid 
Ja 
kuuluvad lennukile 
, st. neid saab kujutada kui 
Ja 
.
Kui vektorite koordinaadid on kirjutatud tabeli kujul järgmiselt: 
, siis võime öelda, et neist moodustub teist järku ruutmaatriks, s.o. suurus 
, mis koosneb kahest reast ja kahest veerust. Igale ruutmaatriksile määratakse arv, mis arvutatakse maatriksi elementide põhjal teatud reeglite järgi ja mida nimetatakse determinandiks. Teist järku maatriksi determinant on võrdne põhidiagonaali ja sekundaarse diagonaali elementide korrutistega:
.
Sel juhul:
Determinandi absoluutväärtus on seega võrdne vektoritele ehitatud rööpküliku pindalaga 
Ja 
nagu külgedel.
Kui võrrelda seda avaldist vektorkorrutise valemiga (4.7), siis:
|
|
See avaldis on valem kolmandat järku maatriksi determinandi arvutamiseks esimesest reast.
Seega:
Kolmandat järku maatriksi determinant arvutatakse järgmiselt:
ja on kuue liikme algebraline summa.
Kolmandat järku maatriksi determinandi arvutamise valemit on lihtne meelde jätta, kui kasutate reegelSarrus, mis on sõnastatud järgmiselt:
Iga termin on kolme elemendi korrutis, mis asuvad maatriksi erinevates veergudes ja erinevates ridades;
Plussmärgil on nende elementide korrutised, mis moodustavad põhidiagonaaliga paralleelse küljega kolmnurgad;
Miinusmärk antakse külgdiagonaalile kuuluvate elementide korrutistele ja elementide kahele korrutisele, mis moodustavad kolmnurgad, mille külg on külgdiagonaaliga paralleelne.
Omadus:
cos 2 α + cos 2 β + cos 2 γ = 1
b) lineaarsete tehete määratlemine
kahe mittekollineaarse vektori summa ja seda nimetatakse vektoriks, mis tuleb vektorite ühisest alguspunktist piki nendele vektoritele ehitatud rööpküliku diagonaali
Vektorite erinevust ja nimetatakse vektori ja vektorile vastupidise vektori summaks: 
. Ühendage vektorite algused ja , siis vektor on suunatud vektori lõpust vektori lõppu . 
tööd vektorit arvule nimetatakse vektoriks mooduliga , ja jaoks ja jaoks . Geomeetriliselt tähendab arvuga korrutamine vektori "venitamist" koefitsiendiga 1, hoides samal ajal suunda ja muutudes vastupidiseks .
Ülaltoodud vektorite lisamise ja arvuga korrutamise reeglitest tulenevad ilmsed väited:
1. 
(liitmine on kommutatiivne);
2. 
(lisamine on assotsiatiivne);
3. 
(nullvektori olemasolu);
4. 
(vastandvektori olemasolu);
5. 
(lisamine on assotsiatiivne);
6. (arvuga korrutamine on distributiivne);
7. 
(vektori liitmine on distributiivne);
c) skalaarkorrutis ja selle peamised omadused
Dot toode Kahe nullist erineva vektori arvu nimetatakse arvuks, mis on võrdne nende vektorite pikkuste ja nendevahelise nurga koosinuse korrutisega. Kui vähemalt üks kahest vektorist on null, siis nendevaheline nurk ei ole määratletud ja skalaarkorrutist loetakse nulliks. Tähistatakse vektorite skalaarkorrutist ja
, kus ja on vektorite pikkused ja vastavalt ning on vektorite vaheline nurk ja .
Vektori skalaarkorrutist iseendaga nimetatakse punktruuduks.
Skalaarkorrutise omadused.
Mis tahes vektorite puhul on tõesed järgmised: punkti toote omadused:
skalaarkorrutise kommutatiivsuse omadus;
jaotusomadus 
või 
;
assotsiatiivne omadus 
või 
, kus on suvaline reaalarv;
vektori skalaarruut on alati mittenegatiivne ja siis ja ainult siis, kui vektor on null.
D) vektorkorrutis ja selle omadused
vektorprodukt vektorit a vektorisse b nimetatakse vektoriks c, mille pikkus on arvuliselt võrdne vektoritele a ja b ehitatud rööpküliku pindalaga, mis on risti nende vektorite tasapinnaga ja on suunatud nii, et väikseim pöörlemine punktist a punktini b vektori c ümber on vastupäeva, vaadatuna lõppvektorist c
Valemid vektorite ristkorrutise arvutamiseks
vektorprodukt kaks vektorit a = (a x ; a y ; a z ) ja b = (b x ; b y ; b z ) Descartes'i koordinaatides on vektor, mille väärtust saab arvutada järgmiste valemite abil:
- Kahe nullist erineva vektori a ja b ristkorrutis on null siis ja ainult siis, kui vektorid on kollineaarsed.
- Vektor c, mis on võrdne nullist erineva vektorite a ja b ristkorrutisega, on nende vektoritega risti.
- a × b = -b × a
- (k a) × b = a × (k b) = k (a × b)
- (a + b) × c = a × c + b × c
Tasapinna sirgjoone võrrand
A) kaldega sirge võrrand
Sirge kalle nimetatakse selle sirge kalde puutujaks.
Sirge kallet tähistatakse tavaliselt tähega k. Siis definitsiooni järgi.
Kui joon on paralleelne y-teljega, siis kallet ei eksisteeri (sel juhul öeldakse, et kalle läheb ka lõpmatusse).
Sirge positiivne kalle näitab selle funktsioonigraafiku suurenemist, negatiivne kahanemist. Kaldjoonega sirge võrrand on kujul y=kx+b, kus k on sirge kalle, b on mingi reaalarv. Sirge võrrand kaldega võib määrata mis tahes sirge, mis ei ole paralleelne Oy teljega (y-teljega paralleelse sirge puhul ei ole kalle määratletud).
B) sirgjooneliste võrrandite tüübid
Võrrand 
helistas sirgjoone üldvõrrand pinnal.
Iga kahe muutujaga esimese astme võrrand x Ja y lahke , Kus A, IN Ja KOOS on mõned reaalarvud ja A Ja IN samaaegselt ei ole võrdne nulliga, määratleb sirge ristkülikukujulises koordinaatsüsteemis Oxy tasapinnal ja iga tasapinna sirge on antud vormi võrrandiga .
Sirge võrrand , kus a Ja b kutsutakse mõnda muud reaalarvu kui null sirgjoone võrrand segmentides. See nimi pole juhuslik, kuna arvude absoluutväärtused A Ja b võrdne nende lõikude pikkustega, mille sirgjoon koordinaattelgedel ära lõikab Ox Ja Oy vastavalt (segmendid loetakse lähtepunktist).
Sirge võrrand , kus x Ja y on muutujad ja k Ja b on mõned reaalarvud, mida nimetatakse sirge võrrand kaldega (k- nurgakoefitsient)
Tasapinna sirge kanooniline võrrand ristkülikukujulises Descartes'i koordinaatsüsteemis Oxy on vorm 
, kus ja on mõned reaalarvud ning ja ei ole samal ajal võrdsed nulliga.
On ilmne, et sirge kanoonilise võrrandiga määratletud sirge läbib punkti. Omakorda on arvud ja , mis seisavad murdude nimetajates, selle sirge suunava vektori koordinaadid. Seega sirge kanooniline võrrand ristkülikukujulises koordinaatsüsteemis Oxy tasapinnal vastab punkti läbivale sirgele, millel on suunavektor .
Tasapinna sirge parameetrilised võrrandid välja nägema 
, kus ja on mõned reaalarvud ning ja ei ole samal ajal võrdsed nulliga ning on parameeter, mis võtab mis tahes reaalväärtusi.
Sirge parameetrilised võrrandid loovad parameetri abil kaudse seose sirge punktide abstsisside ja ordinaatide vahel (sellest ka seda tüüpi sirge võrrandite nimi).
Arvupaar , mis arvutatakse sirge parameetriliste võrrandite abil parameetri mõne reaalväärtuse jaoks, on mõne sirge punkti koordinaadid. Näiteks kui meil on 
, see tähendab, et koordinaatidega punkt asub sirgel.
Tuleb märkida, et sirge parameetrilistes võrrandites olevad koefitsiendid ja parameetri juures on selle sirge suunamisvektori koordinaadid
Kaht punkti läbiva sirge võrrand
Olgu ruumis antud kaks punkti M 1 (x 1, y 1, z 1) ja M 2 (x 2, y 2, z 2), siis neid punkte läbiva sirge võrrand:
Kui mõni nimetajatest on võrdne nulliga, tuleb vastav lugeja määrata võrdseks nulliga Tasapinnal on ülaltoodud sirge võrrand lihtsustatud:
kui x 1 ≠ x 2 ja x = x 1, kui x 1 = x 2.
Murd = k nimetatakse kaldetegur otse.
C) kahe sirge vahelise nurga arvutamine
kui kaks sirget on antud y = k 1 x + b 1 , y = k 2 x + b 2 , siis nende joonte vaheline teravnurk määratletakse järgmiselt
.
Kaks sirget on paralleelsed, kui k 1 = k 2 . Kaks sirget on risti, kui k 1 = -1/ k 2 .
Teoreem. Sirged Ax + Vy + C \u003d 0 ja A 1 x + B 1 y + C 1 \u003d 0 on paralleelsed, kui koefitsiendid A 1 \u003d λA, B 1 \u003d λB on proportsionaalsed. Kui ka С 1 = λС, siis jooned langevad kokku. Nende sirgete võrrandisüsteemi lahendusena leitakse kahe sirge lõikepunkti koordinaadid.
D) kahe sirge paralleelsuse ja perpendikulaarsuse tingimused
Kahe joone paralleelsuse tingimused:
a) Kui sirged on antud kaldega võrranditega, siis on nende paralleelsuse vajalikuks ja piisavaks tingimuseks nende nõlvade võrdsus:
k 1 = k 2 .
b) Juhul, kui sirged on antud võrranditega üldkujul (6), on nende paralleelsuse vajalik ja piisav tingimus, et koefitsiendid vastavatel voolukoordinaatidel nende võrrandites on võrdelised, s.t.
Kahe joone perpendikulaarsuse tingimused:
a) Juhul, kui sirged on antud võrranditega (4) kaldega, on nende perpendikulaarsuse vajalik ja piisav tingimus, et nende kalded on suuruselt pöördsuurused ja vastasmärgilised, s.t.
Selle tingimuse võib kirjutada ka vormile
k 1 k 2 = -1.
b) Kui sirgete võrrandid on antud üldkujul (6), siis nende perpendikulaarsuse tingimuseks (vajalik ja piisav) on võrdsuse täitmine
A 1 A 2 + B 1 B 2 = 0.
Funktsiooni piirang
A) järjestuse piirang
Piiri mõistet kasutasid Newton 17. sajandi teisel poolel ja 18. sajandi matemaatikud, nagu Euler ja Lagrange, kuid nad mõistsid piiri intuitiivselt. Esimesed ranged definitsioonid jada piiri kohta andsid Bolzano 1816. aastal ja Cauchy 1821. aastal.
Numbrile helistatakse numbrilise jada piir, kui jada on lõpmatult väike, st kõik selle elemendid, alates mõnest, on väiksemad kui mis tahes positiivne arv, mis on ette võetud.
Juhul, kui arvulisel jadal on piir reaalarvu kujul, kutsutakse seda koonduvad sellele numbrile. Vastasel juhul nimetatakse jada lahknev . Kui see on pealegi piiramatu, siis eeldatakse, et selle piir on võrdne lõpmatusega.
Lisaks, kui piiramata jada kõik elemendid, alates mõnest arvust, on positiivse märgiga, siis ütleme, et sellise jada piir on võrdne pluss lõpmatus .
Kui piiramatu jada elemendid, mis algavad mõnest arvust, on negatiivse märgiga, siis öeldakse, et sellise jada piir on võrdne miinus lõpmatus .
B) funktsiooni piirang
Funktsiooni piirang (funktsiooni piirang) antud punktis on funktsiooni definitsioonipiirkonda piirav väärtus selline, milleni vaadeldava funktsiooni väärtus kaldub, kui selle argument kaldub antud punkti.
Funktsiooni piirang on jada piiri mõiste üldistus: algselt mõisteti funktsiooni piiri punktis funktsiooni vahemiku elementide jada piiri, mis koosneb elementide jada punktide kujutistest. antud punktile koonduva funktsiooni domeenist (piir, mille juures vaadeldakse); kui selline piir on olemas, siis öeldakse, et funktsioon läheneb määratud väärtusele; kui sellist piiri ei ole, siis öeldakse, et funktsioon lahkneb.
Funktsiooni piirang- üks matemaatilise analüüsi põhimõisteid. Väärtust nimetatakse piiri (piirväärtus) funktsiooni punktis , kui mis tahes punktide jada puhul, mis läheneb punktile , kuid mis ei sisalda selle ühe elemendina (st punkteeritud naabruses ), läheneb funktsiooni väärtuste jada väärtusele .
Väärtust nimetatakse piiri (piirväärtus) funktsiooni punktis , kui mis tahes eelnevalt võetud positiivse arvu korral on sellele vastav positiivne arv, nii et kõigi tingimust täitvate argumentide korral on ebavõrdsus täidetud.
C) kaks tähelepanuväärset piiri
· Esimene tähelepanuväärne piir:
Tagajärjed
· 
· 
· 
· Teine tähelepanuväärne piir:
Tagajärjed
1. 
2. 
3. 
4. 
5. 
jaoks ,
6. 
D) lõpmata väikesed ja lõpmata suured funktsioonid
Funktsioon y=f(x) helistas lõpmatult väike juures x→a või millal x→∞ kui või , s.t. Lõpmata väike funktsioon on funktsioon, mille piirväärtus antud punktis on null.
kui funktsioon y=f(x) esindatav aadressil x→a konstantse arvu summana b ja lõpmata väike α(x): f(x)=b+ α(x) See .
Ja vastupidi, kui , siis f(x)=b+α(x), Kus a(x) on lõpmatult väike juures x→a.
Tagajärg 1. Kui ja , siis .
Tagajärg 2. Kui c= const, siis .
Kui funktsioon f(x) on lõpmatult suur kell x→a, siis funktsioon 1 /f(x) on lõpmatult väike juures x→a.
Kui funktsioon f(x)- lõpmatult väike juures x→a(või x→∞) ja siis ei kao y= 1/f(x) on lõpmatu funktsioon. Lõpmatult väikeste ja lõpmatult suurte funktsioonide lihtsamaid omadusi saab kirjutada järgmiste tingimuslike seoste abil: A≠ 0
D) ebakindluse avalikustamine. L'Hopitali reegel
määramatuse peamised liigid: null jagatud nulliga ( 0 kuni 0), jagage lõpmatus lõpmatusega, korrutage null lõpmatusega, lõpmatus miinus lõpmatus, üks lõpmatuse astmega, null nulli astmega, lõpmatus nulli astmega.
L'Hopitali reegel jaoks kasutatakse väga laialdaselt piirarvutused kui esineb määramatus kujul null jagatud nulliga, lõpmatus jagatud lõpmatusega.
Seda tüüpi määramatused vähendatakse nulli korda lõpmatuseni ja lõpmatus miinus lõpmatus.
Kas ja kui funktsioonid f(x) Ja g(x) on diferentseeruvad punkti läheduses, siis 
Juhul, kui määramatus ei kao pärast L'Hopitali reegli rakendamist, saab seda uuesti rakendada.
Tuletisinstrumentide arvutamine
A) kompleksfunktsiooni diferentseerimise reegel
Las on keeruline funktsioon , kus funktsioon on vaheargument. Näitame, kuidas leida kompleksfunktsiooni tuletist, teades funktsiooni tuletist (tähistame seda ) ja funktsiooni tuletist.
1. teoreem. Kui funktsioonil on punktis tuletis x, ja funktsioonil on tuletis punktis (), siis kompleksfunktsioon punktis x on tuletis ja = .
Vastasel juhul on kompleksfunktsiooni tuletis võrdne antud funktsiooni tuletise korrutisega vaheargumendi suhtes vaheargumendi tuletisega.
B) parameetriliselt antud funktsiooni diferentseerimine
Olgu funktsioon antud parameetrilisel kujul, see tähendab kujul:
kus funktsioonid ja on defineeritud ja pidevad parameetri teatud intervalli jooksul . Leiame iga võrdsuse parema ja vasaku osa diferentsiaalid:
Teise tuletise leidmiseks teostame järgmised teisendused:
C) funktsiooni logaritmilise tuletise mõiste
Positiivse funktsiooni logaritmilist tuletist nimetatakse tuletiseks. Kuna , siis saame kompleksfunktsiooni diferentseerimise reegli kohaselt logaritmilise tuletise jaoks järgmise seose:
.
Logaritmilist tuletist kasutades on mugav arvutada tavatuletist juhtudel, kui logaritm lihtsustab funktsiooni kuju.
Sellise eristamise olemus on järgmine: esmalt leitakse antud funktsiooni logaritm ja alles siis arvutatakse sellest tuletis. Olgu antud mingi funktsioon. Võtame selle avaldise vasaku ja parema külje logaritmi:
Ja siis, väljendades soovitud tuletist, saame tulemuseks:
D) pöördfunktsiooni tuletis
Kui y=f(x) ja x=g(y) on vastastikku pöördfunktsioonide paar ja funktsioonil y=f(x) on tuletis f"(x), siis pöördfunktsiooni g"( x)=1/f" (x).
Seega on vastastikku pöördfunktsioonide tuletised pöördväärtused. Pöördfunktsiooni tuletise valem:
E) implitsiitse funktsiooni tuletis
Kui ühe muutuja funktsiooni kirjeldatakse võrrandiga y=f(x), kus muutuja y on vasakul pool, samas kui parem pool sõltub ainult argumendist x, siis ütleme, et funktsioon on antud selgesõnaliselt. Näiteks on selgesõnaliselt määratletud järgmised funktsioonid:
y= patt x,y=x 2+2x+5,y=lncos x.
Paljudes ülesannetes saab aga funktsiooni anda kaudselt, st. võrrandi kujul
F(x,y)=0.
tuletise leidmiseks y′( x) kaudselt määratletud funktsiooni, ei ole vaja seda eksplitsiitseks teisendada. Selleks, teades võrrandit F(x,y)=0, tehke lihtsalt järgmist:
Esiteks peate eristama võrrandi mõlemad pooled muutuja suhtes x, eeldades et y on diferentseeritav funktsioon x ja kompleksfunktsiooni tuletise arvutamise reegli kasutamine. Sel juhul on nulli tuletis (paremal pool) samuti võrdne nulliga.
Kommenteeri: Kui parem pool on nullist erinev, st. kaudsel võrrandil on vorm
f(x,y)=g(x,y),
siis eristame võrrandi vasakut ja paremat poolt.
Lahendage saadud võrrand tuletise suhtes y′( x).
Tuletise mõiste
A) tuletise määratlus
Funktsiooni tuletis eristamist integratsiooni.
y xx
Tuletisdefinitsioon
Mõelge funktsioonile f(x x 0. Seejärel funktsioon f(x) on eristatav punktis x 0 ja tema tuletis määratakse valemiga
f′( x 0)=limΔ x→0Δ yΔ x=limΔ x→0f(x 0+Δ x)−f(x 0)Δ x.
Funktsiooni tuletis- üks matemaatika põhimõisteid ja matemaatilises analüüsis on tuletis koos integraaliga kesksel kohal. Tuletise leidmise protsessi nimetatakse eristamist. Nimetatakse pöördtehte – funktsiooni taastamine tuntud tuletisest integratsiooni.
Funktsiooni tuletis mingil hetkel iseloomustab funktsiooni muutumise kiirust selles punktis. Muutuse kiiruse hinnangu saab, kui arvutada funktsiooni muutuse Δ suhe y argumendi Δ vastavale muutusele x. Tuletise definitsioonis vaadeldakse sellist suhet limiidis tingimusel Δ x→0. Liigume edasi rangema sõnastuse juurde:
Tuletisdefinitsioon
Mõelge funktsioonile f(x), mille domeen sisaldab punkti ümber mõnda avatud intervalli x 0. Seejärel funktsioon f(x) on eristatav punktis x 0 ja tema tuletis määratakse valemiga
f′( x 0)=limΔ x→0Δ yΔ x=limΔ x→0f(x 0+Δ x)−f(x 0)Δ x.
B) tuletise geomeetriline tähendus
Antud väärtuse jaoks arvutatud funktsiooni tuletis võrdub telje positiivse suuna ja selle funktsiooni graafikule abstsissiga punktis joonistatud puutuja positiivse suunaga moodustatud nurga puutujaga:
Kui funktsioonil on mingis punktis lõplik tuletis, siis naabruses saab seda lähendada lineaarfunktsiooniga
Funktsiooni nimetatakse puutujaks punktis Number.
D) lihtsaimate elementaarfunktsioonide tuletiste tabel
Def. 1.5.6. Suunakoosinused vektor A nimetame nende nurkade koosinusi, mille see vektor moodustab baasvektoritega, i , j , k .
Vektori suuna koosinused A = (X, juures, z) leitakse valemitega:
Suunakoosinuste ruutude summa on võrdne ühega:
Vektori suuna koosinused a
on selle orthi koordinaadid: .
Olgu alusvektorid i , j , k tõmmatud ühisest punktist KOHTA. Eeldame, et ortid määravad telgede positiivsed suunad Oh, OU, Oz. punktide kogumine KOHTA (päritolu) ja ortonormaalne alus i , j , k helistas Descartes'i ristkülikukujuline koordinaatsüsteem ruumis. Lase A on suvaline punkt ruumis. Vektor A = OA= x i + y j + z k helistas raadiuse vektor punktid A, selle vektori koordinaadid ( x, y, z) nimetatakse ka punkti koordinaatideks A(sümbol: A(x, y, z)). Koordinaatide teljed Oh, OU, Oz nimetatakse ka vastavalt teljeks abstsiss, telg ordinaat, telg kohaldada.
Kui vektor on antud selle alguspunkti koordinaatidega IN 1 (x 1 , y 1 , z 1) ja lõpp-punkt IN 2 (x 2 ,
y 2 , z 2), siis on vektori koordinaadid võrdsed lõpu ja alguse koordinaatide vahega: (kuna 
).
Descartes'i ristkülikukujulised koordinaatsüsteemid tasapinnal ja sirgel defineeritakse täpselt samamoodi vastavate kvantitatiivsete (vastavalt dimensioonile) muutustega.
Tüüpiliste ülesannete lahendamine.
Näide 1 Leia vektori pikkuse ja suuna koosinused A = 6i – 2j -3k .
Lahendus. Vektori pikkus: 
. Suuna koosinused: 
.
Näide 2 Otsige vektori koordinaadid A , moodustades koordinaattelgedega võrdsed teravnurgad, kui selle vektori pikkus on võrdne .
Lahendus. Kuna , siis asendades valemiga (1.6), saame 
. Vektor A
moodustab koordinaattelgedega teravad nurgad, seega orto 
. Seetõttu leiame vektori koordinaadid 
.
Näide 3 Antud on kolm mittetasatasandilist vektorit e 1 = 2i – k , e 2 = 3i + 3j , e 3 = 2i + 3k . Lagundada vektorit d = i + 5j - 2k alus e 1 , e 2 , e 3 .
Suunakoosinuste ruutude summa on võrdne ühega.
Kui vektori suunakoosinused on teada, siis saab selle koordinaadid leida valemite abil: Sarnased valemid toimuvad ka kolmemõõtmelisel juhul - kui vektori suunakoosinused on teada, siis saab selle koordinaadid leida ka kolmemõõtmelisel juhul. valemid:
9 Vektorite lineaarne sõltuvus ja lineaarne sõltumatus. Alusel lennukil ja ruumis
Vektorite hulka nimetatakse vektorsüsteem.
lineaarselt sõltuv, kui on numbreid , ei ole kõik korraga võrdsed nulliga, nii et
Vektorite süsteemi nimetatakse lineaarselt sõltumatu, kui võrdsus on võimalik ainult jaoks, s.t. kui võrdsuse vasakul pool olev lineaarne kombinatsioon on triviaalne.
1. Üks vektor moodustab ka süsteemi: at - lineaarselt sõltuv ja at - lineaarselt sõltumatu.
2. Vektorite süsteemi mis tahes osa nimetatakse allsüsteem.
1. Kui vektorite süsteem sisaldab nullvektorit, siis on see lineaarselt sõltuv
2. Kui vektorite süsteemil on kaks võrdset vektorit, siis on see lineaarselt sõltuv.
3. Kui vektorite süsteemis on kaks võrdelist vektorit , siis on see lineaarselt sõltuv.
4. Vektorite süsteem on lineaarselt sõltuv siis ja ainult siis, kui vähemalt üks vektoritest on teiste lineaarne kombinatsioon.
5. Kõik vektorid, mis kuuluvad lineaarselt sõltumatusse süsteemi, moodustavad lineaarselt sõltumatu alamsüsteemi.
6. Lineaarselt sõltuvat alamsüsteemi sisaldav vektorite süsteem on lineaarselt sõltuv.
7. Kui vektorite süsteem on lineaarselt sõltumatu ja peale vektori lisamist sellele osutub see lineaarselt sõltuvaks, siis saab vektorit laiendada vektorites ja pealegi ainulaadsel viisil, s.t. laienduskoefitsiendid leitakse üheselt.
Alus tasapinnal ja ruumis nimetatakse maksimaalseks lineaarselt sõltumatuks vektorite süsteemiks tasapinnal või ruumis (ühe vektori lisamine süsteemi muudab selle lineaarselt sõltuvaks).
Seega on alus tasapinnas mis tahes kaks mittekollineaarset vektorit, mis on võetud teatud järjekorras, ja baas ruumis on mis tahes kolm mittetasapinnalist vektorit, mis on võetud teatud järjekorras.
Olgu ruumis alus, siis T. 3 kohaselt laguneb mis tahes ruumivektor unikaalsel viisil baasvektorite osas: . Laienduskoefitsiente nimetatakse baasis oleva vektori koordinaatideks
Lineaartehte kirjutamine vektoritele koordinaatide järgi:
a) liitmine ja lahutamine: - alus
b) korrutamine arvuga R:
Valemid tulenevad lineaartehte omadusest.
10 vektorkoordinaadid baasi suhtes. Horts
Alus vabade vektorite ruumis V 3 kutsutakse mitte-ühistasandiliste vektorite järjestatud kolmik.
Lase IN :a 1,a 2,a 3 on kindel alus V 3.
Koordinaadid vektor b aluse suhtes IN nimetatakse järjestatud arvude kolmikuks ( x, y, z), sh. b=x· a 1 +ya 2+za 3.
Määramine:b={x, y, z} B Märkus: Fikseeritud vektori koordinaadid on vastava vaba vektori koordinaadid.
Teoreem 1: V 3 ja R 3 vaheline vastavus fikseeritud baasil on üks-ühele, s.o. b V 3 ! {x, y, z) R 3 ja ( x, y, z) R 3! b V 3 , kaasa arvatud b={x, y, z} B
Vektori ja selle koordinaatide vastavusel antud alusel on järgmised omadused:
1. Lase b 1 ={x1, y1, z1} B , b 2 ={x2, y2, z2} B b1 + b2 ={x 1 + x 2, y 1 + y 2, z 1 + z 2} B
2. Lase b={x, y, z} B , λR λ· b={ λ· x, λ· y, λ· z} B
3. Lase b 1 || b 2, b 1 = {x1, y1, z1} B
, b 2 ={x2, y2, z2} B
(Siin: suvaline number).
Ühikuvektor, mis on suunatud piki X-telge, on tähistatud i, ühikvektor, mis on suunatud piki Y-telge, on tähistatud j, A ühikvektor, mis on suunatud piki Z-telge, on tähistatud k. Vektorid i, j, k helistas orts– neil on üksikud moodulid, see tähendab
i = 1, j = 1, k = 1
Vektorite 11 punkti korrutis. Nurk vektorite vahel. Vektorite ortogonaalsuse tingimus
See arv on võrdne nende vektorite pikkuste ja nendevahelise nurga koosinuse korrutisega.
Vektorite punktkorrutis nende koordinaatide järgi
Vektorite punktkorrutis X, Y, Z ja :
kus on nurk vektorite ja ; kui kumbki, siis
Skalaarkorrutise definitsioonist tuleneb, et kus näiteks on vektori projektsiooni väärtus vektori suunale .
Vektori skalaarruut:
Punkti toote omadused:
Nurk vektorite vahel
Vektorite ortogonaalsuse tingimused.
Kaks vektor a ja b ortogonaalne (risti), kui nende skalaarkorrutis on võrdne nulliga a b= 0
Nii ka tasapinnalise vektori ülesande puhul
a= (a x ;a y )ja b= (b x ;b y )
on ortogonaalsed, kui a b= a x b x + a y b y = 0
12 vektorite korrutis, selle omadused. Kollineaarsete vektorite seisund
Vektori ristkorrutis vektoriga on vektor, mida tähistatakse sümboliga ja mis on määratletud järgmise kolme tingimusega:
1). Vektori moodul on , kus on nurk vektorite ja vahel;
2). Vektor on risti iga vektori ja ;
3). Vektori suund vastab "parema käe reeglile". See tähendab, et kui vektorid , ja viia ühisesse algusse, siis tuleb vektorit suunata samamoodi nagu on suunatud parema käe keskmine sõrm, mille pöial on suunatud piki esimest faktorit (st. piki vektorit) ja nimetissõrmega piki teist (st piki vektorit ). Vektorkorrutis sõltub tegurite järjekorrast, nimelt: .
Ristkorrutise moodul on võrdne vektoritele ehitatud rööpküliku pindalaga S ja : .
Vektorkorrutist ennast saab väljendada valemiga,
kus on vektori vektori korrutis.
Vektorkorrutis kaob siis ja ainult siis, kui vektorid ja on kollineaarsed. Eriti, .
Kui koordinaattelgede süsteem on õige ja vektorid ja on antud süsteemis nende koordinaatidega:
siis määratakse vektori ja vektori ristkorrutis valemiga
Vektor on nullist erineva vektori suhtes kollineaarne siis ja ainult siis, kui koordinaadid
vektorid on võrdelised vektori vastavate koordinaatidega s.t.
Sarnaselt sooritatakse lineaarsed toimingud vektoritega, mis on antud nende ruumikoordinaatide järgi.
13 vektorite segakorrutis. Selle omadused. Vektorite komplanaarsuse tingimus
Kolme vektori segakorrutis, , on arv, mis võrdub vektori skalaarkorrutisega vektoriga:
Segatud toote omadused:
3° Kolm vektorit on tasapinnalised siis ja ainult siis
4° Vektorite kolmik on õige siis ja ainult siis, kui . Kui , siis vektorid , ja moodustavad vektorite vasaku kolmiku.
10° Jacobi identiteet:
Kui vektorid ja on antud nende koordinaatidega, siis arvutatakse nende segakorrutis valemiga
Nimetatakse vektoreid, mis on paralleelsed sama tasapinnaga või asuvad samal tasapinnal koplanaarsed vektorid.
Vektorite komplanaarsuse tingimused
Kolm vektorid on tasapinnalised kui nende segaprodukt on null.
Kolm vektorid on tasapinnalised kui need on lineaarselt sõltuvad.
15 erinevat tüüpi sirge ja tasandi võrrandid
Mis tahes tasapinna sirge saab esitada esimest järku võrrandiga
Ah + Wu + C = 0,
ja konstandid A, B ei ole samal ajal võrdsed nulliga. Seda esimest järku võrrandit nimetatakse sirgjoone üldvõrrand. Sõltuvalt konstantide A, B ja C väärtustest on võimalikud järgmised erijuhud:
C \u003d 0, A ≠ 0, B ≠ 0 - joon läbib alguspunkti
A \u003d 0, B ≠ 0, C ≠ 0 (By + C \u003d 0) - joon on paralleelne Ox teljega
B \u003d 0, A ≠ 0, C ≠ 0 ( Ax + C \u003d 0) - joon on paralleelne Oy teljega
B \u003d C \u003d 0, A ≠ 0 - sirgjoon langeb kokku Oy teljega
A \u003d C \u003d 0, B ≠ 0 - sirgjoon langeb kokku Ox teljega
Sirge võrrandit saab esitada erinevates vormides, olenevalt antud lähtetingimustest.
