ये उन कोणों की कोसाइन हैं जो वेक्टर निर्देशांक के सकारात्मक अर्ध-अक्षों के साथ बनाता है। दिशा कोज्या विशिष्ट रूप से वेक्टर की दिशा को परिभाषित करती है। यदि किसी वेक्टर की लंबाई 1 है, तो उसकी दिशा-कोसाइन उसके निर्देशांक के बराबर होती है। सामान्य तौर पर, निर्देशांक वाले एक वेक्टर के लिए ( ए; बी; सी)दिशा कोसाइन बराबर हैं:
जहां ए, बी, जी वेक्टर द्वारा अक्षों के साथ बनाए गए कोण हैं एक्स, य, जेडक्रमश।
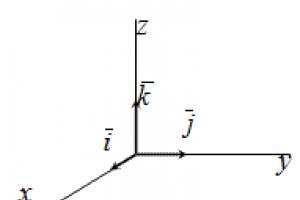
21) सदिश के पदों में एक सदिश का अपघटन। निर्देशांक अक्ष की दिशा को , अक्षों को - द्वारा, अक्षों को - द्वारा निरूपित किया जाता है (चित्र 1)।
समतल में स्थित किसी भी वेक्टर के लिए, निम्नलिखित अपघटन होता है:
यदि वेक्टर 
अंतरिक्ष में स्थित है, तो निर्देशांक अक्षों के इकाई सदिशों के संदर्भ में विस्तार का रूप होता है:
22)डॉट उत्पाददो गैर-शून्य सदिश और इन सदिशों की लंबाई और उनके बीच के कोण की कोज्या के गुणनफल के बराबर संख्या कहलाती है:
23) दो सदिशों के बीच का कोण
यदि दो सदिशों के बीच का कोण न्यून कोण है, तो उनका बिंदु गुणनफल धनात्मक होता है; यदि सदिशों के बीच का कोण अधिक है, तो इन सदिशों का अदिश गुणनफल ऋणात्मक होता है। दो गैर-शून्य सदिशों का अदिश गुणनफल शून्य होता है यदि और केवल यदि ये सदिश ऑर्थोगोनल हों।
24) दो सदिशों की समांतरता और लंबवतता की स्थिति।
सदिशों की लंबवतता की स्थिति
सदिश लंबवत होते हैं यदि और केवल यदि उनका आंतरिक उत्पाद शून्य हो। दो सदिश a(xa;ya) और b(xb;yb) दिए गए हैं। यदि अभिव्यक्ति xaxb + yayb = 0 है तो ये सदिश लंबवत होंगे।
25) दो सदिशों का सदिश गुणनफल।
दो असंरेखीय सदिशों का एक सदिश उत्पाद एक सदिश c=a×b होता है जो निम्नलिखित शर्तों को पूरा करता है: 1) |c|=|a| |बी| syn(a^b) 2) c⊥a, c⊥b 3) सदिश a, b, c सदिशों का दायां त्रिक बनाते हैं।
26) संरेख और समतलीय सदिश..
सदिश संरेख होते हैं यदि पहले सदिश का भुज दूसरे सदिश के भुज से उसी प्रकार संबंधित होता है जैसे पहले की कोटि दूसरे की कोटि से संबंधित होती है। दो सदिश दिए गए हैं ए (एक्सए;फिर) और बी (एक्सबी;वाई बी). ये सदिश संरेख हैं यदि एक्स ए = एक्सबीऔर आप ए = वाई बी, कहाँ आर.
सदिश −→ ए,−→बीऔर −→ सीबुलाया समतलीययदि कोई ऐसा तल मौजूद है जिसके वे समानांतर हैं।
27) तीन सदिशों का मिश्रित गुणनफल। सदिशों का मिश्रित उत्पाद- सदिश a का अदिश गुणनफल और सदिश b और c का सदिश गुणनफल। सदिश a = (1; 2; 3), b = (1; 1; 1), c = (1; 2; 1) का मिश्रित उत्पाद ज्ञात कीजिए।
समाधान:
1 1 1 + 1 1 2 + 1 2 3 - 1 1 3 - 1 1 2 - 1 1 2 = 1 + 2 + 6 - 3 - 2 - 2 = 2
28) एक समतल पर दो बिंदुओं के बीच की दूरी। दो दिए गए बिंदुओं के बीच की दूरी इन बिंदुओं के समान निर्देशांक के वर्ग अंतर के योग के वर्गमूल के बराबर है।
29) इस संबंध में खंड का विभाजन. यदि बिंदु M(x; y) दो दिए गए बिंदुओं ( , ) और ( , ) से गुजरने वाली एक सीधी रेखा पर स्थित है, और संबंध दिया गया है जिसमें बिंदु M खंड को विभाजित करता है, तो बिंदु M के निर्देशांक निर्धारित किए जाते हैं सूत्रों द्वारा
यदि बिंदु M खंड का मध्यबिंदु है, तो इसके निर्देशांक सूत्रों द्वारा निर्धारित किए जाते हैं
30-31. एक सीधी रेखा का ढलानइस सीधी रेखा के ढलान की स्पर्शरेखा कहलाती है। एक सीधी रेखा का ढलान आमतौर पर अक्षर द्वारा दर्शाया जाता है क. फिर परिभाषा के अनुसार
ढलान के साथ रेखा समीकरणका रूप है जहाँ क- सीधी रेखा का कोणीय गुणांक, बीकुछ वास्तविक संख्या है. ढलान वाली एक सीधी रेखा का समीकरण किसी भी सीधी रेखा को निर्धारित कर सकता है जो अक्ष के समानांतर नहीं है ओए(y-अक्ष के समानांतर एक सीधी रेखा के लिए, ढलान परिभाषित नहीं है)।
33. समतल पर एक सीधी रेखा का सामान्य समीकरण। समीकरण टाइप करें 
वहाँ है एक सीधी रेखा का सामान्य समीकरण ऑक्सी. स्थिरांक ए, बी और सी के मूल्यों के आधार पर, निम्नलिखित विशेष मामले संभव हैं:
C = 0, A ≠ 0, B ≠ 0 - रेखा मूल बिंदु से होकर गुजरती है
ए \u003d 0, बी ≠ 0, सी ≠ 0 (बाय + सी \u003d 0) - रेखा ऑक्स अक्ष के समानांतर है
बी = 0, ए ≠ 0, सी ≠ 0 (एक्स + सी = 0) - रेखा ओए अक्ष के समानांतर है
बी \u003d सी \u003d 0, ए ≠ 0 - सीधी रेखा ओए अक्ष के साथ मेल खाती है
ए \u003d सी \u003d 0, बी ≠ 0 - सीधी रेखा ऑक्स अक्ष के साथ मेल खाती है
34.खंडों में एक सीधी रेखा का समीकरणएक आयताकार समन्वय प्रणाली में एक समतल पर ऑक्सीका रूप है जहाँ एऔर बीकुछ गैर-शून्य वास्तविक संख्याएँ हैं। यह नाम आकस्मिक नहीं है, क्योंकि संख्याओं का निरपेक्ष मान होता है एऔर बीउन खंडों की लंबाई के बराबर जो सीधी रेखा निर्देशांक अक्षों पर काटती है बैलऔर ओएक्रमशः (खंडों को मूल से गिना जाता है)। इस प्रकार, खंडों में एक सीधी रेखा का समीकरण किसी चित्र में इस सीधी रेखा को बनाना आसान बनाता है। ऐसा करने के लिए, समतल पर एक आयताकार समन्वय प्रणाली में निर्देशांक के साथ बिंदुओं को चिह्नित करें, और उन्हें एक सीधी रेखा से जोड़ने के लिए एक रूलर का उपयोग करें।
35. एक सीधी रेखा के सामान्य समीकरण का रूप होता है
सीधी रेखा से मूल बिंदु तक की दूरी कहाँ है; अभिलंब से सीधी रेखा और अक्ष के बीच का कोण है।
सामान्य समीकरण को सामान्य समीकरण (1) से सामान्यीकरण कारक से गुणा करके प्राप्त किया जा सकता है, का चिह्न, के चिह्न के विपरीत है, ताकि।
रेखा और निर्देशांक अक्षों के बीच के कोणों की कोज्या को दिशा कोज्या कहा जाता है, रेखा और अक्ष के बीच का कोण है, रेखा और अक्ष के बीच का कोण है:
इस प्रकार, सामान्य समीकरण को इस प्रकार लिखा जा सकता है
बिंदु से दूरी सीधे करने के लिएसूत्र द्वारा निर्धारित किया जाता है 
36. एक बिंदु और एक रेखा के बीच की दूरी की गणना निम्नलिखित सूत्र द्वारा की जाती है: 
जहां x 0 और y 0 बिंदु के निर्देशांक हैं, और A, B और C रेखा के सामान्य समीकरण से गुणांक हैं
37. एक सीधी रेखा के सामान्य समीकरण को सामान्य समीकरण में लाना। इस संदर्भ में समीकरण और समतल, समीकरणों में पदों की संख्या और स्थान के आयाम के अलावा किसी भी चीज़ में एक दूसरे से भिन्न नहीं हैं। इसलिए, सबसे पहले मैं विमान के बारे में सब कुछ बताऊंगा, और अंत में मैं सीधी रेखा के बारे में आरक्षण कर दूंगा।
मान लीजिए कि समतल का सामान्य समीकरण दिया गया है: Ax + By + Cz + D = 0.
;. हमें सिस्टम मिलता है: g;Mc=cosb, MB=cosaआइए इसे सामान्य रूप में लाएं। ऐसा करने के लिए, हम समीकरण के दोनों हिस्सों को सामान्यीकरण कारक एम से गुणा करते हैं। हमें मिलता है: मैक्स + एमवीयू + एमएसजेड + एमडी = 0। इस मामले में, МА=cos;.g;Mc=cosb, MB=cosa हमें सिस्टम मिलता है:
M2 B2=cos2b
M2 C2=cos2g
सिस्टम के सभी समीकरणों को जोड़ने पर, हमें M * (A2 + B2 + C2) \u003d 1 मिलता है। अब केवल M को यहां से व्यक्त करना बाकी है ताकि यह पता चल सके कि इसे लाने के लिए मूल सामान्य समीकरण को किस विशेष सामान्यीकरण कारक से गुणा किया जाना चाहिए। सामान्य रूप में:
एम = - + 1 / रूट केवी ए2 + बी2 + सी2
एमडी हमेशा शून्य से कम होना चाहिए, इसलिए संख्या एम का चिह्न संख्या डी के चिह्न के विपरीत लिया जाता है।
एक सीधी रेखा के समीकरण के साथ, सब कुछ समान है, केवल M के सूत्र से C2 शब्द को हटा दिया जाना चाहिए।
| कुल्हाड़ी + द्वारा + सी.जे + डी = 0, |
38.समतल का सामान्य समीकरण अंतरिक्ष में प्रपत्र का समीकरण कहा जाता है
कहाँ ए 2 + बी 2 + सी 2 ≠ 0 .
कार्टेशियन समन्वय प्रणाली में त्रि-आयामी अंतरिक्ष में, किसी भी विमान को पहली डिग्री (रैखिक समीकरण) के समीकरण द्वारा वर्णित किया जाता है। इसके विपरीत, कोई भी रैखिक समीकरण एक तल को परिभाषित करता है।
40.खंडों में एक विमान का समीकरण.एक आयताकार समन्वय प्रणाली में ऑक्सीज़त्रि-आयामी अंतरिक्ष में, रूप का एक समीकरण 
, कहाँ ए, बीऔर सीशून्य के अतिरिक्त अन्य वास्तविक संख्याएँ कहलाती हैं खंडों में समतल समीकरण. संख्याओं का निरपेक्ष मान ए, बीऔर सीउन खंडों की लंबाई के बराबर जो विमान निर्देशांक अक्षों पर काटता है बैल, ओएऔर आउंसक्रमशः, मूल से गिनती। संख्या चिह्न ए, बीऔर सीदिखाता है कि निर्देशांक अक्षों पर खंड किस दिशा (सकारात्मक या नकारात्मक) में अंकित हैं
41) समतल का सामान्य समीकरण.
किसी समतल का सामान्य समीकरण उसका समीकरण होता है, जिसे प्रपत्र में लिखा जाता है
जहां , , समतल के अभिलंब की दिक् कोज्याएं हैं, ई
p मूल बिंदु से समतल तक की दूरी है। सामान्य की दिशा कोसाइन की गणना करते समय, यह माना जाना चाहिए कि यह मूल से विमान की ओर निर्देशित है (यदि विमान मूल से गुजरता है, तो सामान्य की सकारात्मक दिशा का विकल्प उदासीन है)।
42) एक बिंदु से एक समतल तक की दूरी।मान लीजिए कि समतल समीकरण द्वारा दिया गया है 
और एक अंक दिया. फिर एक बिंदु से एक समतल तक की दूरी सूत्र द्वारा निर्धारित की जाती है
 |
सबूत. एक बिंदु से एक विमान की दूरी, परिभाषा के अनुसार, एक बिंदु से एक विमान पर गिराए गए लंबवत की लंबाई है
समतलों के बीच का कोण
मान लीजिए कि तलों को क्रमशः समीकरणों तथा द्वारा दिया जाता है। इन तलों के बीच का कोण ज्ञात करना आवश्यक है।
समतल, प्रतिच्छेद करते हुए, चार डायहेड्रल कोण बनाते हैं: दो अधिक और दो न्यून कोण या चार सीधे, और दोनों अधिक कोण एक दूसरे के बराबर होते हैं, और दोनों न्यून कोण भी एक दूसरे के बराबर होते हैं। हम सदैव न्यून कोण की तलाश करेंगे। इसका मान निर्धारित करने के लिए, हम समतलों की प्रतिच्छेदन रेखा पर और प्रत्येक में इस बिंदु पर एक बिंदु लेते हैं
समतलों पर हम प्रतिच्छेदन रेखा पर लंब खींचते हैं।
मान लीजिए एक वेक्टर दिया गया है. यूनिट वेक्टर उसी दिशा में 
(वेक्टर वेक्टर 
) सूत्र द्वारा पाया जाता है:
.
चलो अक्ष 
निर्देशांक अक्षों के साथ कोण बनाता है 
.अक्ष की दिशा कोसाइन 
इन कोणों की कोज्याएँ कहलाती हैं: यदि दिशा 
यूनिट वेक्टर द्वारा दिया गया 
, तो दिशा कोज्या इसके निर्देशांक के रूप में कार्य करती है, अर्थात:
.
दिशा कोसाइन संबंध से संबंधित हैं:
यदि दिशा 
एक मनमाना वेक्टर द्वारा दिया गया 
, फिर इस वेक्टर का इकाई वेक्टर ढूंढें और इसकी तुलना इकाई वेक्टर के लिए अभिव्यक्ति से करें 
, पाना:
अदिश उत्पाद
डॉट उत्पाद
दो वैक्टर 
और 
उनके बीच के कोण की कोज्या द्वारा उनकी लंबाई के गुणनफल के बराबर संख्या कहलाती है: 
.
अदिश उत्पाद में निम्नलिखित गुण होते हैं:
इस तरह, 
.
अदिश उत्पाद का ज्यामितीय अर्थ: वेक्टर और यूनिट वेक्टर का डॉट उत्पाद 
वेक्टर के प्रक्षेपण के बराबर 
निर्धारित दिशा में 
, अर्थात। 
.
अदिश गुणनफल की परिभाषा से ओर्ट्स के गुणन की निम्नलिखित तालिका इस प्रकार है 
:
.
यदि सदिश उनके निर्देशांक द्वारा दिए गए हैं 
और 
, अर्थात। 
,
, फिर, इन सदिशों को अदिश रूप से गुणा करके और ऑर्ट्स की गुणन तालिका का उपयोग करके, हम अदिश गुणनफल के लिए व्यंजक प्राप्त करते हैं 
सदिशों के निर्देशांक के माध्यम से:
.
वेक्टर उत्पाद
एक वेक्टर का क्रॉस उत्पाद
प्रति वेक्टर 
वेक्टर कहा जाता है 
, जिसकी लंबाई और दिशा शर्तों द्वारा निर्धारित की जाती है:
वेक्टर उत्पाद में निम्नलिखित गुण हैं:
पहले तीन गुणों से यह निष्कर्ष निकलता है कि सदिशों के योग का सदिश गुणन सदिशों के योग से बहुपद गुणन के सामान्य नियमों का पालन करता है। केवल यह सुनिश्चित करना आवश्यक है कि गुणकों का क्रम न बदले।
मूल इकाई सदिशों को इस प्रकार गुणा किया जाता है:
अगर 
और 
, फिर सदिशों के सदिश उत्पाद के गुणों को ध्यान में रखते हुए, हम कारक सदिशों के निर्देशांकों से सदिश उत्पाद के निर्देशांक की गणना के लिए एक नियम प्राप्त कर सकते हैं:
यदि हम ऊपर प्राप्त ओर्ट्स के गुणन के नियमों को ध्यान में रखते हैं, तो:
यदि हम एक मैट्रिक्स निर्धारक की अवधारणा का परिचय देते हैं तो दो वैक्टरों के वेक्टर उत्पाद के निर्देशांक की गणना के लिए एक अभिव्यक्ति लिखने का एक अधिक कॉम्पैक्ट रूप बनाया जा सकता है।
एक विशेष मामले पर विचार करें जब सदिश 
और 
विमान के हैं 
, अर्थात। उन्हें इस रूप में दर्शाया जा सकता है 
और 
.
यदि सदिशों के निर्देशांक तालिका के रूप में इस प्रकार लिखे जाएं: 
, तो हम कह सकते हैं कि उनसे दूसरे क्रम का एक वर्ग मैट्रिक्स बनता है, अर्थात। आकार 
, दो पंक्तियों और दो स्तंभों से मिलकर बना है। प्रत्येक वर्ग मैट्रिक्स को एक संख्या निर्दिष्ट की जाती है जिसकी गणना कुछ नियमों के अनुसार मैट्रिक्स के तत्वों से की जाती है और इसे निर्धारक कहा जाता है। दूसरे क्रम के मैट्रिक्स का निर्धारक मुख्य विकर्ण और द्वितीयक विकर्ण के तत्वों के उत्पादों के बीच अंतर के बराबर है:
.
इस मामले में:
इस प्रकार सारणिक का निरपेक्ष मान सदिशों पर बने समांतर चतुर्भुज के क्षेत्रफल के बराबर होता है 
और 
जैसे पक्षों पर.
यदि हम इस अभिव्यक्ति की तुलना वेक्टर उत्पाद सूत्र (4.7) से करें, तो:
|
|
यह अभिव्यक्ति पहली पंक्ति से तीसरे क्रम के मैट्रिक्स के निर्धारक की गणना करने का एक सूत्र है।
इस प्रकार:
तृतीय क्रम मैट्रिक्स निर्धारककी गणना इस प्रकार की जाती है:
और छह पदों का बीजगणितीय योग है।
यदि आप उपयोग करते हैं तो तीसरे क्रम के मैट्रिक्स के निर्धारक की गणना करने का सूत्र याद रखना आसान है नियमसारस, जिसे इस प्रकार तैयार किया गया है:
प्रत्येक पद मैट्रिक्स के विभिन्न स्तंभों और विभिन्न पंक्तियों में स्थित तीन तत्वों का उत्पाद है;
धन चिह्न में उन तत्वों का गुणनफल होता है जो मुख्य विकर्ण के समानांतर भुजा वाले त्रिभुज बनाते हैं;
ऋण चिह्न पार्श्व विकर्ण से संबंधित तत्वों के गुणनफल और पार्श्व विकर्ण के समानांतर भुजा वाले त्रिभुज बनाने वाले तत्वों के दो उत्पादों को दिया जाता है।
संपत्ति:
कॉस 2 α + कॉस 2 β + कॉस 2 γ = 1
बी) रैखिक संचालन की परिभाषा
दो असंरेख सदिशों का योग और इन सदिशों पर बने समांतर चतुर्भुज के विकर्ण के अनुदिश सदिशों के सामान्य मूल से आने वाला सदिश कहलाता है
सदिशों के अंतर को सदिश और सदिश के विपरीत सदिश का योग कहा जाता है: 
. वेक्टर की शुरुआत को कनेक्ट करें और, फिर वेक्टर को वेक्टर के अंत से वेक्टर के अंत तक निर्देशित किया जाता है। 
काम किसी संख्या के वेक्टर को मॉड्यूल के साथ वेक्टर कहा जाता है, और के लिए और के लिए। ज्यामितीय रूप से, किसी संख्या से गुणा करने का मतलब वेक्टर को 1 के कारक से "खींचना" है, जबकि दिशा को बनाए रखना और विपरीत दिशा में बदलना है।
सदिशों को जोड़ने और उन्हें किसी संख्या से गुणा करने के उपरोक्त नियमों से, स्पष्ट कथन इस प्रकार हैं:
1. 
(जोड़ क्रमविनिमेय है);
2. 
(जोड़ साहचर्य है);
3. 
(शून्य वेक्टर का अस्तित्व);
4. 
(विपरीत वेक्टर का अस्तित्व);
5. 
(जोड़ साहचर्य है);
6. (किसी संख्या से गुणा वितरणात्मक होता है);
7. 
(वेक्टर जोड़ वितरणात्मक है);
ग) अदिश उत्पाद और उसके मुख्य गुण
डॉट उत्पाददो गैर-शून्य सदिशों की वह संख्या, जो इन सदिशों की लंबाई और उनके बीच के कोण की कोज्या के गुणनफल के बराबर होती है, कहलाती है। यदि दो सदिशों में से कम से कम एक शून्य है, तो उनके बीच का कोण परिभाषित नहीं है, और अदिश गुणनफल शून्य माना जाता है। सदिशों का अदिश गुणनफल निरूपित किया जाता है
, जहां और क्रमशः सदिशों की लंबाई हैं, तथा सदिशों और के बीच का कोण है।
किसी सदिश के स्वयं के अदिश गुणनफल को बिंदु वर्ग कहा जाता है।
अदिश उत्पाद के गुण.
किसी भी वेक्टर के लिए निम्नलिखित सत्य हैं: डॉट उत्पाद गुण:
अदिश उत्पाद की क्रमविनिमेयता संपत्ति;
वितरण संपत्ति 
या 
;
संबंधी संपत्ति 
या 
, एक मनमाना वास्तविक संख्या कहां है;
किसी सदिश का अदिश वर्ग हमेशा गैर-ऋणात्मक होता है, और यदि और केवल यदि सदिश शून्य होता है।
डी) वेक्टर उत्पाद और उसके गुण
वेक्टर उत्पादवेक्टर ए से वेक्टर बी को वेक्टर सी कहा जाता है, जिसकी लंबाई संख्यात्मक रूप से वेक्टर ए और बी पर बने समांतर चतुर्भुज के क्षेत्र के बराबर होती है, जो इन वैक्टरों के विमान के लंबवत होती है और निर्देशित होती है ताकि ए से बी तक कम से कम घुमाव हो वेक्टर c के चारों ओर वामावर्त है, जब अंत वेक्टर c से देखा जाता है
वैक्टर के क्रॉस उत्पाद की गणना के लिए सूत्र
वेक्टर उत्पादकार्टेशियन निर्देशांक में दो वैक्टर a = (a x ; a y ; a z ) और b = (b x ; b y ; b z ) एक वेक्टर है जिसका मान निम्नलिखित सूत्रों का उपयोग करके गणना की जा सकती है:
- दो अशून्य सदिशों a और b का क्रॉस उत्पाद शून्य है यदि और केवल यदि सदिश संरेख हैं।
- वेक्टर c, जो गैर-शून्य वैक्टर a और b के क्रॉस उत्पाद के बराबर है, इन वैक्टरों के लंबवत है।
- ए × बी = -बी × ए
- (के ए) × बी = ए × (के बी) = के (ए × बी)
- (ए + बी) × सी = ए × सी + बी × सी
समतल पर एक सीधी रेखा का समीकरण
ए) ढलान के साथ एक सीधी रेखा का समीकरण
एक सीधी रेखा का ढलानइस सीधी रेखा के ढलान की स्पर्शरेखा कहलाती है।
एक सीधी रेखा का ढलान आमतौर पर अक्षर द्वारा दर्शाया जाता है क. फिर परिभाषा के अनुसार.
यदि रेखा y-अक्ष के समानांतर है, तो ढलान मौजूद नहीं है (इस मामले में, ढलान को अनंत तक जाने के लिए भी कहा जाता है)।
एक सीधी रेखा का सकारात्मक ढलान इसके फ़ंक्शन ग्राफ़ में वृद्धि को इंगित करता है, एक नकारात्मक ढलान कमी को इंगित करता है। ढलान वाली एक सीधी रेखा के समीकरण का रूप y=kx+b है, जहां k रेखा का ढलान है, b कुछ वास्तविक संख्या है। ढलान वाली एक सीधी रेखा का समीकरण किसी भी सीधी रेखा को निर्दिष्ट कर सकता है जो ओए अक्ष के समानांतर नहीं है (y-अक्ष के समानांतर एक सीधी रेखा के लिए, ढलान परिभाषित नहीं है)।
बी) सीधी रेखा समीकरणों के प्रकार
समीकरण 
बुलाया एक सीधी रेखा का सामान्य समीकरणसतह पर.
दो चरों वाला प्रथम डिग्री का कोई भी समीकरण एक्सऔर यदयालु , कहाँ ए, मेंऔर साथकुछ वास्तविक संख्याएँ हैं, और एऔर मेंएक साथ शून्य के बराबर नहीं, एक आयताकार समन्वय प्रणाली में एक सीधी रेखा को परिभाषित करता है ऑक्सीसमतल पर, और समतल पर कोई भी सीधी रेखा एक समीकरण के रूप में दी जाती है .
सीधी रेखा समीकरण, कहाँ एऔर बीशून्य के अलावा कुछ वास्तविक संख्याओं को कहा जाता है खंडों में एक सीधी रेखा का समीकरण. यह नाम आकस्मिक नहीं है, क्योंकि संख्याओं का निरपेक्ष मान होता है एऔर बीउन खंडों की लंबाई के बराबर जो सीधी रेखा निर्देशांक अक्षों पर काटती है बैलऔर ओएक्रमशः (खंडों को मूल से गिना जाता है)।
सीधी रेखा समीकरण, कहाँ एक्सऔर यचर हैं, और कऔर बीकुछ वास्तविक संख्याएँ कहलाती हैं ढलान के साथ एक सीधी रेखा का समीकरण (क- कोणीय गुणांक)
एक समतल में एक सीधी रेखा का विहित समीकरणएक आयताकार कार्टेशियन समन्वय प्रणाली में ऑक्सीरूप है 
, जहां और कुछ वास्तविक संख्याएं हैं, और तथा एक ही समय में शून्य के बराबर नहीं हैं।
यह स्पष्ट है कि सीधी रेखा के विहित समीकरण द्वारा परिभाषित सीधी रेखा, बिंदु से होकर गुजरती है। बदले में, भिन्नों के हर में स्थित संख्याएँ और, इस रेखा के दिशात्मक सदिश के निर्देशांक हैं। इस प्रकार, रेखा का विहित समीकरण आयताकार समन्वय प्रणाली में ऑक्सीसमतल पर बिंदु से गुजरने वाली और दिशा वेक्टर वाली एक सीधी रेखा से मेल खाती है।
एक समतल पर एक सीधी रेखा के पैरामीट्रिक समीकरणहमशक्ल 
, जहां और कुछ वास्तविक संख्याएं हैं, और तथा एक ही समय में शून्य के बराबर नहीं हैं, और एक पैरामीटर है जो कोई भी वास्तविक मान लेता है।
एक सीधी रेखा के पैरामीट्रिक समीकरण एक पैरामीटर का उपयोग करके सीधी रेखा के बिंदुओं के भुज और निर्देशांक के बीच एक अंतर्निहित संबंध स्थापित करते हैं (इसलिए इस प्रकार की सीधी रेखा समीकरणों का नाम)।
संख्याओं की एक जोड़ी, जिसकी गणना पैरामीटर के कुछ वास्तविक मान के लिए सीधी रेखा के पैरामीट्रिक समीकरणों द्वारा की जाती है, सीधी रेखा पर कुछ बिंदु के निर्देशांक हैं। उदाहरण के लिए, जब हमारे पास 
अर्थात्, निर्देशांक वाला बिंदु एक सीधी रेखा पर स्थित होता है।
यह ध्यान दिया जाना चाहिए कि सीधी रेखा के पैरामीट्रिक समीकरणों में गुणांक और पैरामीटर इस सीधी रेखा के निर्देशन वेक्टर के निर्देशांक हैं
दो बिंदुओं से गुजरने वाली एक रेखा का समीकरण
मान लीजिए अंतरिक्ष में दो बिंदु M 1 (x 1, y 1, z 1) और M 2 (x 2, y 2, z 2) दिए गए हैं, तो इन बिंदुओं से गुजरने वाली एक सीधी रेखा का समीकरण:
यदि कोई भी हर शून्य के बराबर है, तो संबंधित अंश को शून्य के बराबर सेट किया जाना चाहिए। समतल पर, ऊपर लिखा गया सीधी रेखा समीकरण सरल है:
यदि x 1 ≠ x 2 और x = x 1 यदि x 1 = x 2।
भिन्न = k कहा जाता है ढलान कारकसीधा।
सी) दो रेखाओं के बीच के कोण की गणना करना
यदि दो रेखाएँ दी गई हैं y = k 1 x + b 1 , y = k 2 x + b 2 , तो इन रेखाओं के बीच का न्यून कोण इस प्रकार परिभाषित किया जाएगा
.
यदि k 1 = k 2 हो तो दो रेखाएँ समानांतर होती हैं। यदि k 1 = -1/ k 2 है तो दो रेखाएँ लंबवत हैं।
प्रमेय.सीधी रेखाएँ Ax + Vy + C \u003d 0 और A 1 x + B 1 y + C 1 \u003d 0 समानांतर हैं जब गुणांक A 1 \u003d λA, B 1 \u003d λB आनुपातिक हैं। यदि С 1 = λС भी हो, तो रेखाएँ संपाती होती हैं। दो रेखाओं के प्रतिच्छेदन बिंदु के निर्देशांक इन रेखाओं के समीकरणों की प्रणाली के समाधान के रूप में पाए जाते हैं।
डी) दो रेखाओं की समांतरता और लंबवतता की स्थितियां
दो रेखाओं की समानता के लिए शर्तें:
ए) यदि रेखाएँ ढलान वाले समीकरणों द्वारा दी गई हैं, तो उनकी समानता के लिए आवश्यक और पर्याप्त शर्त उनकी ढलानों की समानता है:
क 1 = क 2 .
बी) उस स्थिति के लिए जब रेखाएँ सामान्य रूप (6) में समीकरणों द्वारा दी जाती हैं, उनकी समानता के लिए आवश्यक और पर्याप्त शर्त यह है कि उनके समीकरणों में संबंधित वर्तमान निर्देशांक पर गुणांक आनुपातिक हैं, अर्थात।
दो रेखाओं की लंबता के लिए शर्तें:
ए) उस स्थिति में जब रेखाएं ढलान के साथ समीकरण (4) द्वारा दी गई हैं, तो उनकी लंबवतता के लिए आवश्यक और पर्याप्त शर्त यह है कि उनकी ढलान परिमाण में पारस्परिक और संकेत में विपरीत हैं, यानी।
इस शर्त को फॉर्म में भी लिखा जा सकता है
क 1 क 2 = -1.
बी) यदि सीधी रेखाओं के समीकरण सामान्य रूप (6) में दिए गए हैं, तो उनकी लंबवतता (आवश्यक और पर्याप्त) की शर्त समानता को पूरा करना है
ए 1 ए 2 + बी 1 बी 2 = 0.
कार्य सीमा
ए) अनुक्रम सीमा
सीमा की अवधारणा का उपयोग 17वीं शताब्दी के उत्तरार्ध में न्यूटन द्वारा और 18वीं शताब्दी के यूलर और लैग्रेंज जैसे गणितज्ञों द्वारा किया गया था, लेकिन उन्होंने सीमा को सहज रूप से समझा। अनुक्रम की सीमा की पहली कठोर परिभाषा 1816 में बोल्ज़ानो द्वारा और 1821 में कॉची द्वारा दी गई थी।
नंबर पर कॉल किया जाता है संख्यात्मक अनुक्रम की सीमा, यदि अनुक्रम असीम रूप से छोटा है, यानी, इसके सभी तत्व, कुछ से शुरू होकर, पहले से ली गई किसी भी सकारात्मक संख्या से कम हैं।
ऐसी स्थिति में जब किसी संख्यात्मक अनुक्रम की वास्तविक संख्या के रूप में एक सीमा होती है, तो उसे कहा जाता है अभिसारी इस नंबर पर. अन्यथा, अनुक्रम कहा जाता है विभिन्न . इसके अलावा, यदि यह असीमित है, तो इसकी सीमा अनंत के बराबर मानी जाती है।
इसके अलावा, यदि किसी संख्या से प्रारंभ करके किसी असीमित अनुक्रम के सभी तत्वों पर एक सकारात्मक चिह्न है, तो हम कहते हैं कि ऐसे अनुक्रम की सीमा बराबर है प्लस अनंत .
यदि किसी संख्या से शुरू होने वाले असीमित अनुक्रम के तत्वों पर ऋणात्मक चिह्न हो, तो वे कहते हैं कि ऐसे अनुक्रम की सीमा बराबर है शून्य से अनंत .
बी) कार्य सीमा
कार्य सीमा (कार्य सीमा) किसी दिए गए बिंदु पर, किसी फ़ंक्शन की परिभाषा के क्षेत्र के लिए सीमित करना, एक ऐसा मान है जिस पर विचाराधीन फ़ंक्शन का मान तब जाता है जब उसका तर्क किसी दिए गए बिंदु पर जाता है।
कार्य सीमाएक अनुक्रम की सीमा की अवधारणा का एक सामान्यीकरण है: प्रारंभ में, एक बिंदु पर एक फ़ंक्शन की सीमा को एक फ़ंक्शन की सीमा के तत्वों के अनुक्रम की सीमा के रूप में समझा जाता था, जो तत्वों के अनुक्रम के बिंदुओं की छवियों से बना होता है किसी फ़ंक्शन के डोमेन का किसी दिए गए बिंदु पर अभिसरण (वह सीमा जिस पर विचार किया जाता है); यदि ऐसी कोई सीमा मौजूद है, तो फ़ंक्शन को निर्दिष्ट मान पर अभिसरण करने के लिए कहा जाता है; यदि ऐसी कोई सीमा मौजूद नहीं है, तो फ़ंक्शन को विचलन कहा जाता है।
कार्य सीमा- गणितीय विश्लेषण की बुनियादी अवधारणाओं में से एक। मान कहा जाता है आप LIMIT (सीमा मूल्य) एक बिंदु पर एक फ़ंक्शन का, यदि बिंदुओं के किसी भी अनुक्रम के लिए अभिसरण होता है, लेकिन इसके तत्वों में से एक के रूप में शामिल नहीं होता है (अर्थात, एक छिद्रित पड़ोस में), तो फ़ंक्शन के मानों का अनुक्रम परिवर्तित हो जाता है।
मान कहा जाता है आप LIMIT (सीमा मूल्य) किसी फ़ंक्शन के बिंदु पर, यदि पहले से ली गई किसी भी सकारात्मक संख्या के लिए उसके अनुरूप एक सकारात्मक संख्या होती है, जैसे कि शर्त को संतुष्ट करने वाले सभी तर्कों के लिए, असमानता संतुष्ट होती है।
सी) दो उल्लेखनीय सीमाएँ
· पहली उल्लेखनीय सीमा:
नतीजे
· 
· 
· 
· दूसरी उल्लेखनीय सीमा:
नतीजे
1. 
2. 
3. 
4. 
5. 
के लिए ,
6. 
डी) अतिसूक्ष्म और अपरिमित रूप से बड़े फलन
समारोह y=f(x)बुलाया बहुत छोतापर एक्स→एया जब एक्स→∞ यदि या , अर्थात्। इनफिनिटिमल फ़ंक्शन एक ऐसा फ़ंक्शन है जिसकी किसी दिए गए बिंदु पर सीमा शून्य है।
यदि फ़ंक्शन y=f(x)पर प्रतिनिधित्व करने योग्य एक्स→एएक स्थिर संख्या के योग के रूप में बीऔर असीम रूप से छोटा α(x): f(x)=b+ α(x)वह ।
इसके विपरीत, यदि, तो f(x)=b+α(x), कहाँ ए(एक्स)पर असीम रूप से छोटा है एक्स→ए.
परिणाम 1.यदि और , तो .
परिणाम 2.अगर सी=स्थिरांक, फिर .
यदि फ़ंक्शन एफ(एक्स)पर असीम रूप से बड़ा है एक्स→ए, फिर फ़ंक्शन 1 /एफ(एक्स)पर असीम रूप से छोटा है एक्स→ए.
यदि फ़ंक्शन एफ(एक्स)- असीम रूप से छोटा एक्स→ए(या x→∞)और फिर गायब नहीं होता आप= 1/एफ(एक्स)एक अनंत कार्य है. निम्नलिखित सशर्त संबंधों का उपयोग करके असीम रूप से छोटे और असीम रूप से बड़े कार्यों के सबसे सरल गुण लिखे जा सकते हैं: ए≠ 0
डी) अनिश्चितताओं का खुलासा. एल हॉस्पिटल का नियम
अनिश्चितताओं के मुख्य प्रकार: शून्य को शून्य से विभाजित किया गया ( 0 से 0), अनंत को अनंत से विभाजित करें, शून्य को अनंत से गुणा करें, अनंत को अनंत से घटाएं, एक को अनंत की घात से, शून्य को शून्य की घात से, अनंत को शून्य की घात से।
एल हॉस्पिटल का नियमके लिए बहुत व्यापक रूप से उपयोग किया जाता है गणना सीमित करेंजब शून्य को शून्य से विभाजित करने, अनंत को अनंत से विभाजित करने के रूप में अनिश्चितता होती है।
इस प्रकार की अनिश्चितताएँ शून्य से अनंत तक और अनंत से अनंत तक कम हो जाती हैं।
यदि और यदि कार्य करता है एफ(एक्स)और जी(एक्स)फिर, बिंदु के पड़ोस में अवकलनीय हैं 
ऐसी स्थिति में जब एल'हॉपिटल नियम लागू करने के बाद भी अनिश्चितता दूर नहीं होती है, तो इसे दोबारा लागू किया जा सकता है।
डेरिवेटिव की गणना
ए) एक जटिल कार्य के विभेदन का नियम
चलो है जटिल कार्य , जहां फ़ंक्शन एक मध्यवर्ती तर्क है। हम दिखाएंगे कि किसी जटिल फ़ंक्शन का व्युत्पन्न कैसे खोजा जाए, फ़ंक्शन के लिए व्युत्पन्न (हम इसे इसके द्वारा निरूपित करेंगे) और फ़ंक्शन के लिए व्युत्पन्न को जानते हुए।
प्रमेय 1. यदि किसी फ़ंक्शन का एक बिंदु पर व्युत्पन्न है एक्स, और फ़ंक्शन का बिंदु () पर एक व्युत्पन्न है, फिर बिंदु पर जटिल फ़ंक्शन है एक्सएक व्युत्पन्न है, और =।
अन्यथा, एक जटिल फ़ंक्शन का व्युत्पन्न मध्यवर्ती तर्क के व्युत्पन्न द्वारा मध्यवर्ती तर्क के संबंध में दिए गए फ़ंक्शन के व्युत्पन्न के उत्पाद के बराबर होता है।
बी) पैरामीट्रिक रूप से दिए गए फ़ंक्शन का विभेदन
मान लीजिए कि फ़ंक्शन को पैरामीट्रिक रूप में दिया गया है, अर्थात, इस रूप में:
जहां फ़ंक्शन और पैरामीटर के एक निश्चित अंतराल पर परिभाषित और निरंतर होते हैं। आइए प्रत्येक समानता के दाएं और बाएं भागों से अंतर खोजें:
दूसरा व्युत्पन्न खोजने के लिए, हम निम्नलिखित परिवर्तन करते हैं:
सी) किसी फ़ंक्शन के लघुगणकीय व्युत्पन्न की अवधारणा
किसी धनात्मक फलन के लघुगणकीय व्युत्पन्न को व्युत्पन्न कहा जाता है। चूँकि, एक जटिल फलन के विभेदीकरण के नियम के अनुसार, हम लघुगणकीय व्युत्पन्न के लिए निम्नलिखित संबंध प्राप्त करते हैं:
.
लघुगणक व्युत्पन्न का उपयोग करना, उन मामलों में सामान्य व्युत्पन्न की गणना करना सुविधाजनक है जहां लघुगणक फ़ंक्शन के रूप को सरल बनाता है।
इस तरह के भेदभाव का सार इस प्रकार है: सबसे पहले, दिए गए फ़ंक्शन का लघुगणक पाया जाता है, और उसके बाद ही उससे व्युत्पन्न की गणना की जाती है। कोई फंक्शन दिया जाए. हम इस अभिव्यक्ति के बाएँ और दाएँ पक्षों का लघुगणक लेते हैं:
और फिर, वांछित व्युत्पन्न को व्यक्त करते हुए, परिणामस्वरूप हमारे पास है:
डी) व्युत्क्रम फलन का व्युत्पन्न
यदि y=f(x) और x=g(y) परस्पर व्युत्क्रम कार्यों की एक जोड़ी है, और फ़ंक्शन y=f(x) का व्युत्पन्न f"(x) है, तो व्युत्क्रम फ़ंक्शन g का व्युत्पन्न"( x)=1/f" (x).
इस प्रकार, परस्पर व्युत्क्रम फलनों के व्युत्पन्न व्युत्क्रम होते हैं। व्युत्क्रम फलन के व्युत्पन्न का सूत्र:
ई) एक अंतर्निहित फ़ंक्शन का व्युत्पन्न
यदि एक चर के कार्य को समीकरण द्वारा वर्णित किया गया है य=एफ(एक्स), जहां चर यबाईं ओर है, जबकि दाईं ओर केवल तर्क पर निर्भर करता है एक्स, तो हम कहते हैं कि फ़ंक्शन दिया गया है स्पष्ट रूप से. उदाहरण के लिए, निम्नलिखित फ़ंक्शन स्पष्ट रूप से परिभाषित हैं:
य=पाप एक्स,य=एक्स 2+2एक्स+5,य=lncos एक्स.
हालाँकि, कई कार्यों में फ़ंक्शन दिया जा सकता है उलझाव से, अर्थात। एक समीकरण के रूप में
एफ(एक्स,य)=0.
व्युत्पन्न खोजने के लिए य′( एक्स) एक अंतर्निहित परिभाषित फ़ंक्शन के, इसे स्पष्ट रूप में परिवर्तित करने की कोई आवश्यकता नहीं है। इसके लिए समीकरण जान रहे हैं एफ(एक्स,य)=0, बस निम्न कार्य करें:
सबसे पहले, आपको चर के संबंध में समीकरण के दोनों पक्षों को अलग करना होगा एक्स, ये मानते हुए यएक भिन्न कार्य है एक्सऔर एक जटिल फ़ंक्शन के व्युत्पन्न की गणना के लिए नियम का उपयोग करना। इस स्थिति में, शून्य का व्युत्पन्न (दाईं ओर) भी शून्य के बराबर होगा।
टिप्पणी: यदि दाहिना भाग गैर-शून्य है, अर्थात। अंतर्निहित समीकरण का रूप है
एफ(एक्स,य)=जी(एक्स,य),
फिर हम समीकरण के बाएँ और दाएँ पक्षों को अलग करते हैं।
व्युत्पन्न के संबंध में परिणामी समीकरण को हल करें य′( एक्स).
व्युत्पन्न की अवधारणा
ए) व्युत्पन्न की परिभाषा
फ़ंक्शन व्युत्पन्न भेदभाव एकीकरण.
य एक्सएक्स
व्युत्पन्न परिभाषा
फ़ंक्शन पर विचार करें एफ(एक्स एक्स 0. फिर फ़ंक्शन एफ(एक्स) है विभेदकबिंदु पर एक्स 0 और वह यौगिकसूत्र द्वारा निर्धारित किया जाता है
एफ′( एक्स 0)=limΔ एक्स→0Δ यΔ एक्स=limΔ एक्स→0एफ(एक्स 0+Δ एक्स)−एफ(एक्स 0)Δ एक्स.
फ़ंक्शन व्युत्पन्न- गणित की बुनियादी अवधारणाओं में से एक, और गणितीय विश्लेषण में, व्युत्पन्न, अभिन्न के साथ, एक केंद्रीय स्थान रखता है। व्युत्पन्न ज्ञात करने की प्रक्रिया कहलाती है भेदभाव. व्युत्क्रम संक्रिया - ज्ञात व्युत्पन्न से किसी फ़ंक्शन की पुनर्स्थापना - कहलाती है एकीकरण.
किसी बिंदु पर किसी फ़ंक्शन का व्युत्पन्न उस बिंदु पर फ़ंक्शन के परिवर्तन की दर को दर्शाता है। परिवर्तन की दर का अनुमान फ़ंक्शन परिवर्तन के अनुपात की गणना करके प्राप्त किया जा सकता है यतर्क में संगत परिवर्तन के लिए Δ एक्स. व्युत्पन्न की परिभाषा में, ऐसे अनुपात को शर्त के तहत सीमा में माना जाता है एक्स→0. आइए अधिक कठोर सूत्रीकरण की ओर आगे बढ़ें:
व्युत्पन्न परिभाषा
फ़ंक्शन पर विचार करें एफ(एक्स), जिसके डोमेन में बिंदु के चारों ओर कुछ खुला अंतराल होता है एक्स 0. फिर फ़ंक्शन एफ(एक्स) है विभेदकबिंदु पर एक्स 0 और वह यौगिकसूत्र द्वारा निर्धारित किया जाता है
एफ′( एक्स 0)=limΔ एक्स→0Δ यΔ एक्स=limΔ एक्स→0एफ(एक्स 0+Δ एक्स)−एफ(एक्स 0)Δ एक्स.
बी) व्युत्पन्न का ज्यामितीय अर्थ
किसी दिए गए मान के लिए गणना किए गए फ़ंक्शन का व्युत्पन्न अक्ष की सकारात्मक दिशा और भुज के साथ बिंदु पर इस फ़ंक्शन के ग्राफ़ पर खींची गई स्पर्शरेखा की सकारात्मक दिशा से बने कोण के स्पर्शरेखा के बराबर है:
यदि किसी फ़ंक्शन का एक बिंदु पर परिमित व्युत्पन्न है, तो पड़ोस में इसे एक रैखिक फ़ंक्शन द्वारा अनुमानित किया जा सकता है
फ़ंक्शन को बिंदु संख्या पर स्पर्शरेखा कहा जाता है।
डी) सबसे सरल प्राथमिक कार्यों के डेरिवेटिव की तालिका
हार। 1.5.6. दिशा कोसाइनवेक्टर ए आइए क्रमशः उन कोणों की कोज्याएँ कहते हैं जिन्हें यह वेक्टर आधार वैक्टर के साथ बनाता है, मैं , जे , क .
वेक्टर दिशा कोसाइन ए = (एक्स, पर, जेड) सूत्रों द्वारा पाए जाते हैं:
दिशा कोज्या के वर्गों का योग एक के बराबर होता है:
वेक्टर दिशा कोसाइन ए
इसके ऑर्थ के निर्देशांक हैं: .
चलो आधार वैक्टर मैं , जे , क एक सामान्य बिंदु से खींचा गया के बारे में. हम मान लेंगे कि ओर्ट्स अक्षों की सकारात्मक दिशाएँ निर्धारित करते हैं ओह, कहां, आउंस. बिंदु संग्रह के बारे में (मूल) और एक लम्बवत् आधार मैं , जे , क बुलाया अंतरिक्ष में कार्टेशियन आयताकार समन्वय प्रणाली. होने देना एअंतरिक्ष में एक मनमाना बिंदु है. वेक्टर ए = ओए= एक्स मैं + य जे + जेड क बुलाया त्रिज्या सदिशअंक ए, इस वेक्टर के निर्देशांक ( एक्स, य, जेड) को बिंदु निर्देशांक भी कहा जाता है ए(प्रतीक: ए(एक्स, य, जेड)). समायोजन ध्रुव ओह, कहां, आउंसक्रमशः अक्ष भी कहा जाता है सूच्याकार आकृति का भुज, एक्सिस तालमेल, एक्सिस आवेदन करें.
यदि वेक्टर को उसके प्रारंभिक बिंदु के निर्देशांक द्वारा दिया गया है में 1 (एक्स 1 , य 1 , जेड 1) और अंतिम बिंदु में 2 (एक्स 2 ,
य 2 , जेड 2), तो वेक्टर के निर्देशांक अंत और शुरुआत के निर्देशांक के बीच के अंतर के बराबर हैं: (चूंकि 
).
समतल और रेखा पर कार्तीय आयताकार समन्वय प्रणालियाँठीक उसी तरह से संबंधित मात्रात्मक (आयाम के अनुसार) परिवर्तनों के साथ परिभाषित किया गया है।
विशिष्ट कार्यों का समाधान.
उदाहरण 1एक वेक्टर की लंबाई और दिशा कोसाइन ज्ञात करें ए = 6मैं – 2जे -3क .
समाधान।वेक्टर लंबाई: 
. दिशा कोसाइन: 
.
उदाहरण 2वेक्टर निर्देशांक खोजें ए , जो निर्देशांक अक्षों के साथ समान न्यून कोण बनाता है, यदि इस वेक्टर की लंबाई बराबर है।
समाधान।चूँकि, फिर सूत्र (1.6) में प्रतिस्थापित करने पर, हम प्राप्त करते हैं 
. वेक्टर ए
निर्देशांक अक्षों के साथ तीव्र कोण बनाता है, इसलिए ऑर्थो 
. इसलिए, हम वेक्टर के निर्देशांक पाते हैं 
.
उदाहरण 3तीन गैर-समतलीय सदिश दिए गए हैं इ 1 = 2मैं – क , इ 2 = 3मैं + 3जे , इ 3 = 2मैं + 3क . वेक्टर विघटित करें डी = मैं + 5जे - 2क आधार इ 1 , इ 2 , इ 3 .
दिशा कोज्या के वर्गों का योग एक के बराबर होता है।
यदि सदिश की दिशा-कोज्या ज्ञात हो, तो उसके निर्देशांक सूत्रों द्वारा ज्ञात किये जा सकते हैं: इसी प्रकार के सूत्र त्रि-आयामी मामले में भी होते हैं - यदि वेक्टर की दिशा-कोज्या ज्ञात हो, तो उसके निर्देशांक सूत्र द्वारा ज्ञात किये जा सकते हैं सूत्र:
9 सदिशों की रैखिक निर्भरता और रैखिक स्वतंत्रता। विमान और अंतरिक्ष में आधार
सदिशों के समुच्चय को कहा जाता है वेक्टर प्रणाली.
रैखिक रूप से निर्भर, यदि संख्याएँ हैं, तो सभी एक ही समय में शून्य के बराबर नहीं हैं, जैसे कि
सदिशों की प्रणाली कहलाती है रैखिक रूप से स्वतंत्र,यदि समानता केवल के लिए संभव है, अर्थात जब समानता के बाईं ओर रैखिक संयोजन तुच्छ है।
1. एक वेक्टर भी एक प्रणाली बनाता है: at - रैखिक रूप से निर्भर, और at - रैखिक रूप से स्वतंत्र।
2. सदिशों की प्रणाली के किसी भी भाग को कहा जाता है सबसिस्टम.
1. यदि सदिशों की प्रणाली में शून्य सदिश शामिल है, तो यह रैखिक रूप से निर्भर है
2. यदि सदिशों की एक प्रणाली में दो समान सदिश हैं, तो यह रैखिक रूप से निर्भर है।
3. यदि सदिशों की एक प्रणाली में दो आनुपातिक सदिश हैं, तो यह रैखिक रूप से निर्भर है।
4. सदिशों की एक प्रणाली रैखिक रूप से निर्भर होती है यदि और केवल तभी जब कम से कम एक सदिश अन्य सदिशों का रैखिक संयोजन हो।
5. रैखिक रूप से स्वतंत्र प्रणाली में शामिल कोई भी वेक्टर एक रैखिक रूप से स्वतंत्र उपप्रणाली बनाता है।
6. रैखिक रूप से निर्भर उपप्रणाली वाले वैक्टर की एक प्रणाली रैखिक रूप से निर्भर होती है।
7. यदि वैक्टर की प्रणाली रैखिक रूप से स्वतंत्र है, और इसमें एक वेक्टर जोड़ने के बाद यह रैखिक रूप से निर्भर हो जाता है, तो वेक्टर को वैक्टर में विस्तारित किया जा सकता है, और, इसके अलावा, एक अनोखे तरीके से, यानी। विस्तार गुणांक विशिष्ट रूप से पाए जाते हैं।
आधारसमतल और अंतरिक्ष पर समतल या अंतरिक्ष में सदिशों की अधिकतम रैखिक रूप से स्वतंत्र प्रणाली कहलाती है (प्रणाली में एक और सदिश जोड़ने से यह रैखिक रूप से निर्भर हो जाता है)।
इस प्रकार, समतल में एक आधार एक निश्चित क्रम में लिए गए कोई दो गैर-समरेखीय सदिश होते हैं, और अंतरिक्ष में एक आधार एक निश्चित क्रम में लिए गए कोई तीन गैर-समरेखीय सदिश होते हैं।
मान लीजिए कि अंतरिक्ष में एक आधार है, तो, टी. 3 के अनुसार, किसी भी अंतरिक्ष वेक्टर को आधार वैक्टर के संदर्भ में एक अनोखे तरीके से विघटित किया जाता है:। विस्तार गुणांक को आधार में वेक्टर के निर्देशांक कहा जाता है
निर्देशांक के संदर्भ में सदिशों पर रैखिक संक्रियाएँ लिखना:
a) जोड़ और घटाव:- आधार
बी) संख्या आर से गुणा:
सूत्र रैखिक संक्रियाओं के गुण से अनुसरण करते हैं।
10 वेक्टर आधार के सापेक्ष समन्वय करता है। हॉर्ट्स
आधारमुक्त सदिशों के स्थान में वि 3गैर-समतलीय सदिशों के किसी भी क्रमित त्रिक को कहा जाता है।
होने देना में :एक 1,एक 2,एक 3में एक निश्चित आधार है वि 3.
COORDINATESवेक्टर बीआधार के सापेक्ष में संख्याओं का क्रमित त्रिक कहा जाता है ( एक्स, वाई, जेड), सहित। बी=एक्स· एक 1+यए 2+जेडएक 3 .
पद का नाम:बी={एक्स, वाई, जेड} बी नोट: एक निश्चित वेक्टर के निर्देशांक संबंधित मुक्त वेक्टर के निर्देशांक होते हैं।
प्रमेय 1:एक निश्चित आधार के लिए वी 3 और आर 3 के बीच पत्राचार एक-से-एक है, यानी। बी वि 3 ! {एक्स, वाई, जेड) आर 3 और ( एक्स, वाई, जेड) आर 3 ! बी वी 3 ,शामिल बी={एक्स, वाई, जेड} बी
किसी दिए गए आधार पर एक वेक्टर और उसके निर्देशांक के बीच पत्राचार में निम्नलिखित गुण होते हैं:
1. होने देना बी 1 ={X1, y1, z1} बी , बी 2 ={x2, y2, z2} बी बी1 + बी2 ={x 1 + x 2 , y 1 + y 2 , z 1 + z 2} बी
2. होने देना बी={एक्स, वाई, जेड} बी , λR λ· बी={ λ· एक्स, λ· हाँ, λ· जेड} बी
3. चलो बी 1 || बी 2 , बी 1 = {X1, y1, z1} बी
, बी 2 ={x2, y2, z2} बी
(यहां: कोई भी संख्या)।
इकाई वेक्टर, एक्स अक्ष के साथ निर्देशित, दर्शाया गया है मैं, इकाई वेक्टर, Y अक्ष के अनुदिश निर्देशित, निरूपित है जे, ए इकाई वेक्टर, Z अक्ष के अनुदिश निर्देशित, निरूपित है क. वैक्टर मैं, जे, कबुलाया ओर्ट्स- उनके पास एकल मॉड्यूल हैं, अर्थात
मैं = 1, जे = 1, के = 1
सदिशों का 11 बिंदु गुणनफल। सदिशों के बीच का कोण. सदिशों की रूढ़िवादिता की स्थिति
यह संख्या इन सदिशों की लंबाई और उनके बीच के कोण की कोज्या के गुणनफल के बराबर है।
उनके निर्देशांक के संदर्भ में वैक्टर का डॉट उत्पाद
वैक्टर का डॉट उत्पादएक्स, वाई, जेड और:
सदिशों और के बीच का कोण कहां है; यदि कोई है, तो
अदिश उत्पाद की परिभाषा से यह पता चलता है कि, उदाहरण के लिए, वेक्टर की दिशा पर वेक्टर के प्रक्षेपण का मान कहां है।
एक सदिश का अदिश वर्ग:
डॉट उत्पाद गुण:
सदिशों के बीच का कोण
सदिशों की रूढ़िवादिता के लिए शर्तें.
दो वेक्टरए और बी ओर्थोगोनल (लंबवत), यदि उनका अदिश गुणनफल शून्य a b= 0 के बराबर है
तो एक समतल सदिश समस्या के मामले में
a= (a x ;a y )और b= (b x ;b y )
ऑर्थोगोनल हैं यदि a b= a x b x + a y b y = 0
12 सदिशों का सदिश गुणनफल, उसके गुण। संरेख सदिशों की स्थिति
एक वेक्टर द्वारा एक वेक्टर का क्रॉस उत्पाद एक वेक्टर होता है जिसे प्रतीक द्वारा दर्शाया जाता है और निम्नलिखित तीन स्थितियों द्वारा परिभाषित किया जाता है:
1). वेक्टर का मॉड्यूल है, जहां वेक्टर और के बीच का कोण है;
2). वेक्टर प्रत्येक वेक्टर के लंबवत है और;
3). वेक्टर की दिशा "दाहिने हाथ के नियम" से मेल खाती है। इसका मतलब यह है कि यदि वेक्टर, और को एक सामान्य शुरुआत में लाया जाता है, तो वेक्टर को उसी तरह निर्देशित किया जाना चाहिए जैसे दाहिने हाथ की मध्य उंगली को निर्देशित किया जाता है, जिसका अंगूठा पहले कारक के साथ निर्देशित होता है (अर्थात, वेक्टर के साथ), और तर्जनी दूसरी के साथ (अर्थात, वेक्टर के साथ)। वेक्टर उत्पाद कारकों के क्रम पर निर्भर करता है, अर्थात्:।
क्रॉस उत्पाद का मॉड्यूल वैक्टर और : पर बने समांतर चतुर्भुज के क्षेत्र एस के बराबर है।
वेक्टर उत्पाद स्वयं सूत्र द्वारा व्यक्त किया जा सकता है,
वेक्टर वेक्टर उत्पाद कहां है.
सदिश उत्पाद लुप्त हो जाता है यदि और केवल यदि सदिश और संरेख हों। विशेष रूप से, ।
यदि निर्देशांक अक्षों की प्रणाली सही है और इस प्रणाली में सदिश उनके निर्देशांक द्वारा दिए गए हैं:
फिर एक वेक्टर और एक वेक्टर का क्रॉस उत्पाद सूत्र द्वारा निर्धारित किया जाता है
एक सदिश एक अशून्य सदिश के संरेख होता है यदि और केवल यदि निर्देशांक हों
सदिश सदिश के संगत निर्देशांक के समानुपाती होते हैं, अर्थात।
अंतरिक्ष में उनके निर्देशांक द्वारा दिए गए वैक्टर पर रैखिक संचालन समान रूप से किया जाता है।
13 सदिशों का मिश्रित गुणनफल। इसके गुण. वैक्टर के लिए अनुरूपता की स्थिति
तीन सदिशों का मिश्रित गुणनफल, , एक सदिश द्वारा एक सदिश के अदिश गुणनफल के बराबर एक संख्या है:
मिश्रित उत्पाद गुण:
3° तीन सदिश समतलीय हैं यदि और केवल यदि
4° सदिशों का एक त्रिक सही है यदि और केवल यदि। यदि , तो सदिश , और सदिशों का बायाँ त्रिक बनाते हैं।
10° जैकोबी पहचान:
यदि सदिश, और उनके निर्देशांक द्वारा दिए गए हैं, तो उनके मिश्रित उत्पाद की गणना सूत्र द्वारा की जाती है
वे सदिश जो एक ही तल के समानांतर होते हैं या एक ही तल पर स्थित होते हैं, कहलाते हैं समतलीय सदिश.
वैक्टर के लिए अनुरूपता की शर्तें
तीन सदिश समतलीय होते हैंयदि उनका मिश्रित उत्पाद शून्य है।
तीन सदिश समतलीय होते हैंयदि वे रैखिक रूप से निर्भर हैं।
15 एक सीधी रेखा और एक तल के विभिन्न प्रकार के समीकरण
समतल में कोई भी रेखा प्रथम कोटि समीकरण द्वारा दी जा सकती है
आह + वू + सी = 0,
और स्थिरांक A, B एक ही समय में शून्य के बराबर नहीं हैं। इस प्रथम कोटि समीकरण को कहा जाता है एक सीधी रेखा का सामान्य समीकरण.स्थिरांक ए, बी और सी के मूल्यों के आधार पर, निम्नलिखित विशेष मामले संभव हैं:
C = 0, A ≠ 0, B ≠ 0 - रेखा मूल बिंदु से होकर गुजरती है
ए \u003d 0, बी ≠ 0, सी ≠ 0 (बाय + सी \u003d 0) - रेखा ऑक्स अक्ष के समानांतर है
बी = 0, ए ≠ 0, सी ≠ 0 (एक्स + सी = 0) - रेखा ओए अक्ष के समानांतर है
बी \u003d सी \u003d 0, ए ≠ 0 - सीधी रेखा ओए अक्ष के साथ मेल खाती है
ए \u003d सी \u003d 0, बी ≠ 0 - सीधी रेखा ऑक्स अक्ष के साथ मेल खाती है
किसी भी प्रारंभिक स्थिति के आधार पर एक सीधी रेखा के समीकरण को विभिन्न रूपों में प्रस्तुत किया जा सकता है।
